Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

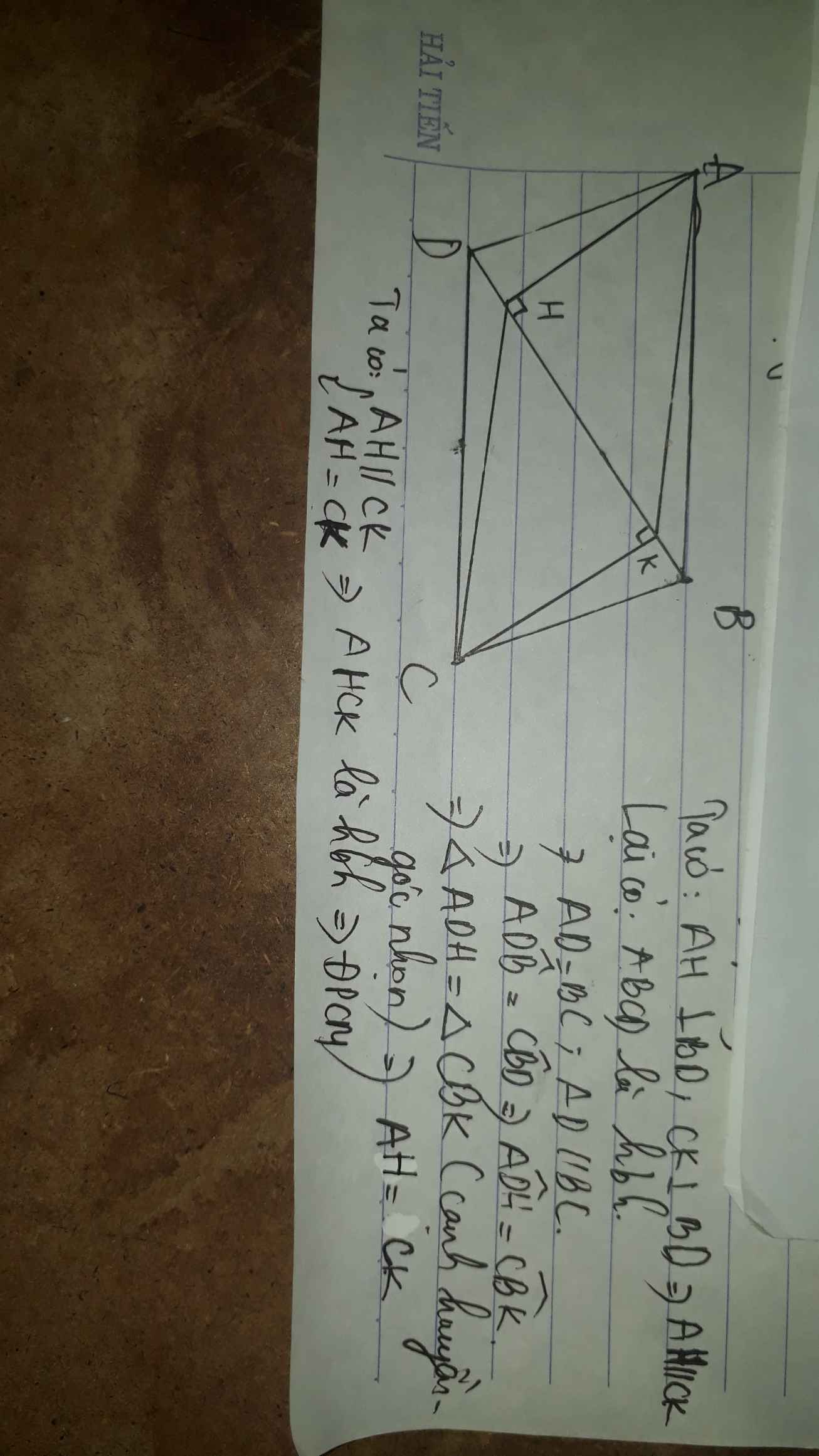
a: Xét ΔADH vuông tại H và ΔCBK vuông tại K có
AD=BC
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔADH=ΔCBK
Suy ra:AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành

Bài 3:
a: Ta có: AD+DB=AB
AE+EC=AC
mà DB=EC và AB=AC
nên AD=AE
Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
nên DE//BC
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
Hình thang BDEC có \(\widehat{DBC}=\widehat{ECB}\)
nên BDEC là hình thang cân
b: Để BD=DE=EC thì BD=DE và DE=EC
BD=DE thì ΔDBE cân tại D
=>\(\widehat{DBE}=\widehat{DEB}\)
mà \(\widehat{DEB}=\widehat{EBC}\)(hai góc so le trong, DE//BC)
nên \(\widehat{DBE}=\widehat{EBC}\)
=>\(\widehat{ABE}=\widehat{EBC}\)
=>BE là phân giác của góc ABC
=>E là chân đường phân giác kẻ từ B xuống AC
Xét ΔEDC có ED=EC
nên ΔEDC cân tại E
=>\(\widehat{EDC}=\widehat{ECD}\)
mà \(\widehat{EDC}=\widehat{DCB}\)(hai góc so le trong, DE//BC)
nên \(\widehat{ECD}=\widehat{DCB}\)
=>\(\widehat{ACD}=\widehat{BCD}\)
=>CD là phân giác của góc ACB
=>D là chân đường phân giác từ C kẻ xuống AB
Bài 2:
a: Ta có: ABCD là hình bình hành
=>AB//CD và AB=CD(1)
Ta có: M là trung điểm của AB
=>\(AM=MB=\dfrac{AB}{2}\left(2\right)\)
Ta có: N là trung điểm của CD
=>\(NC=ND=\dfrac{CD}{2}\left(3\right)\)
Từ (1),(2),(3) suy ra AM=MB=NC=ND
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b: Ta có AMCN là hình bình hành
=>AN//CM
Xét ΔDFC có
N là trung điểm của DC
NE//FC
Do đó: E là trung điểm của DF
=>DE=EF(4)
Xét ΔABE có
M là trung điểm của BA
MF//AE
Do đó: F là trung điểm của BE
=>BF=FE(5)
Từ (4) và (5) suy ra BF=FE=ED

a: Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔAHD=ΔCKB
Suy ra: AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
b: Ta có: AHCK là hình bình hành
nên Hai đường chéo AC và HK cắt nhau tại trung điểm của mỗi đường
mà O là trung điểm của HK
nên O là trung điểm của AC
hay A,O,C thẳng hàng

Ta chứng minh AH//CK, AH = CK (DAHD = DCKB) Þ AHCK là hình bình hành (cặp cạnh đối song song và bằng nhau)


Ta có DAOK = DCOH Þ OK =OH, DDOE = DBOF Þ OE = OF Þ EHFK là hình bình hành


a: Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
góc ADH=góc CBK
=>ΔAHD=ΔCKB
=>AH=CK
mà AH//CK
nên AHCK là hình bình hành
b: AHCK là hbh
=>AC cắt HK tại trung điểm của mỗi đường
=>A,O,C thẳng hàng

Lời giải:
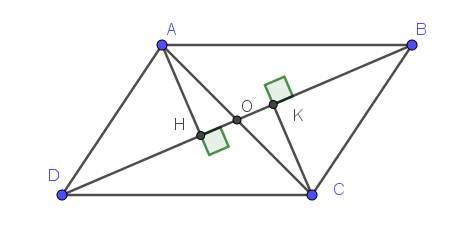
Vì $ABCD$ là hình bình hành nên $AO=OC$
Xét tam giác $AHO$ và $CKO$ có:
$\widehat{AHO}=\widehat{CKO}=90^0$
$\widehat{AOH}=\widehat{COK}$ (đối đỉnh)
$AO=CO$
$\Rightarrow \triangle AHO=\triangle CKO$ (ch-gn)
$\Rightarrow AH=CK$
Tứ giác $AHCK$ có 2 cạnh đối $AH, CK$ song song (do cùng vg với $BD$) và bằng nhau nên $AHCK$ là hbh.