Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài 1) ta có \(\overrightarrow{AQ}=\overrightarrow{AM}+\overrightarrow{MN}+\overrightarrow{NP}+\overrightarrow{PQ}=\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{DC}+\overrightarrow{BC}\)
\(=\left(\overrightarrow{BA}+\overrightarrow{BC}\right)+\left(\overrightarrow{DA}+\overrightarrow{DC}\right)=\overrightarrow{BD}+\overrightarrow{DB}=\overrightarrow{0}\left(đpcm\right)\)
bài 2) bn tham khảo nha : https://hoc24.vn/hoi-dap/question/636668.html

Câu 1: A
$\overrightarrow{BA}-\overrightarrow{BC}+\overrightarrow{DC}=\overrightarrow{CA}+\overrightarrow{DC}=\overrightarrow{DA}=\overrightarrow{CB}$
Câu 2:
$\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{DB}$
$=\overrightarrow{DC}+\overrightarrow{CB}$
$\Rightarrow \overrightarrow{AB}-\overrightarrow{DC}=\overrightarrow{CB}+\overrightarrow{AD}$
$\Rightarrow \overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}$
Đáp án A.

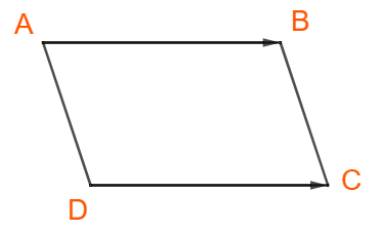
a) ABCD là hình bình hành nên \(\overrightarrow {DC} = \overrightarrow {AB} \)
\( \Rightarrow \overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {BA} + \overrightarrow {AB} = \overrightarrow {BB} = \overrightarrow 0 \)
b) \(\overrightarrow {MA} + \overrightarrow {MC} = \left( {\overrightarrow {MB} + \overrightarrow {BA} } \right) + \left( {\overrightarrow {MD} + \overrightarrow {DC} } \right)\)
\(= \left( {\overrightarrow {MB} + \overrightarrow {MD} } \right) + \left( {\overrightarrow {BA} + \overrightarrow {DC}} \right)\)
\(= \overrightarrow {MB} + \overrightarrow {MD} \) (Vì \(\overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {0} \))




Do \(\overrightarrow{NP}=\overrightarrow{DC}\); \(\overrightarrow{AM}=\overrightarrow{BA}\Rightarrow\overrightarrow{MA}=\overrightarrow{AB}\).
Do tứ giác ABCD là hình bình hành nên \(\overrightarrow{AB}=\overrightarrow{DC}\).
Vì vậy \(\overrightarrow{NP}=\overrightarrow{MA}\) nên tứ giác NPAM là hình bình hành.
Vì vậy \(\overrightarrow{PA}=\overrightarrow{NM}\). (1)
Mà \(\overrightarrow{MN}=\overrightarrow{DA}\) suy ra \(\overrightarrow{NM}=\overrightarrow{AD}\) . (2)
Mặt khác \(\overrightarrow{AD}=\overrightarrow{BC}\) (do tứ giác ABCD là hình bình hành). (3)
Từ (1);(2);(3) suy ra:\(\overrightarrow{PA}=\overrightarrow{BC}\).
Mà \(\overrightarrow{PQ}=\overrightarrow{BC}\Rightarrow\overrightarrow{PQ}=\overrightarrow{PA}\).
Vì vậy hai điểm A và Q trùng nhau nên \(\overrightarrow{AQ}=\overrightarrow{0}\).