Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABD có
E là trung điểm của AB
H là trung điểm của AD
Do đó: EH là đường trung bình của ΔABD
Suy ra: EH//BD và \(EH=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
F là trung điểm của BC
G là trung điểm của DC
Do đó: FG là đường trung bình của ΔBCD
Suy ra: FG//BD và \(FG=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra EH//GF và EH=GF
hay EHGF là hình bình hành

AE//CG, AE = CG nên AECG là hình bình hành ⇒ O là trung điểm của EG. Tương tự O là trung điểm của HF.

Tâm đối xứng của hình bình hành ABCD là giao điểm O của các đường chéo AC và BD.

E, F lần lượt là trung điểm của AB và BC (gt)
\(\Rightarrow\) EF là đường trung bình của tam giác ABC
\(\Rightarrow\) EF // AC và EF = \(\frac{1}{2}\) AC (1)
H, G lần lượt là trung điểm của AD và DC (gt)
\(\Rightarrow\) HG là đường trung bình của tam giác ACD
\(\Rightarrow\) HG // AC và HG = \(\frac{1}{2}\) AC (2)
Từ (1) và (2) \(\Rightarrow\) EF // HG và EF = HG
\(\Rightarrow\) Tứ giác EFGH là hình bình hành
Tứ giác EFGH là hình bình hành. EF // AC, EF = \(\frac{1}{2}\) AC
Ta còn có EH là đường trung bình của tam giác ABD
\(\Rightarrow\) EH // BD và EH = \(\frac{1}{2}\) BD
- Tứ giác EFGH là hình chữ nhật
\(\Leftrightarrow\) Hình bình hành EFGH có:
\(\widehat{HEF}=90^o\)
\(\Leftrightarrow HE\perp EF\)
\(\Leftrightarrow EH\perp AC\)
\(\Leftrightarrow AC\perp BD\)
Vậy tứ giác ABCD cần thêm điều kiện hai đường chéo AC và BD vuông góc với nhau thì tứ giác EFGH là hình chữ nhật
- Tứ giác EFGH là hình thoi
\(\Leftrightarrow\) Hình bình hành EFGH có: EF = EH \(\Leftrightarrow\) AC = BD
Vậy tứ giác ABCD cần thêm điều kiện hai đường chéo AC và BD bằng nhau thì tứ giác EFGH là hình thoi
- Tứ giác EFGH là hình vuông
\(\Leftrightarrow\) Hình chữ nhật EFGH có: EF = EH \(\Leftrightarrow\) AC = BD
Vậy tứ giác ABCD cần thêm điều kiện hai đường chéo AC và BD vuông góc và bằng nhau thì tứ giác EFGH là hình vuông

O còn là tâm đối xứng của các hình bình hành: AECG, EBGD, AHCF, DHBF.

a: Xét ΔBAD có
M,Q lần lượt là tđiểm của AB và AD
nên MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N,P lần lượt là trung điểm của CB và CD
nên NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy a MQ//NP và MQ=NP
=>MNPQ là hình bình hành
b: Xét ΔABC có
M,N lần lượt là trung điểm của BA và BC
nên MN là đường trung bình
=>MN=AC/2 và MN//AC
Để MNPQ là hình chữ nhật thì MN vuông góc với MQ
=>AC vuông góc với BD

a) nối A với C , B với D được:
EF // AC ( đường trung bình của tam giác BAC)
HG // AC ( " " " " " " ) suy ra EF // AC do cùng // AC
HE // DB ( đường trung bình tam giác ADB )
FG // DB ( " " " " " " ) suy ra HE // FG do cùng // với DB
Xét tứ giác EFGH có 2 cặp cạnh đối song song nên EFGH là hình bình hành
b) EFGH là hình ....
Thoi , suy ra EH = GH nên AC=BD ( do là đường trung bình của hai tam giác ADB,ADC)
vì AC = BD nên ABCD là hình thang cân
Chữ nhật, suy ra HE vuông góc với HG nên AC vuông góc với BD
Hình vuông , kết hợp 2 yếu tố của 2 hình trên được AC=BD và AC vuông góc với BD.
Tích nha☺
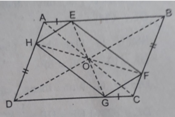
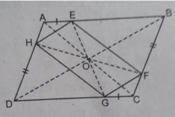
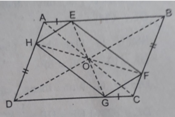
Tứ giác EFGH