Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Độ dài trung đoạn của hình chóp S.ABC là độ dài đoạn thẳng từ trung điểm của cạnh đáy đến đỉnh của hình chóp. Vì tam giác ABC là tam giác đều, nên ta có thể tính độ dài trung đoạn bằng cách sử dụng công thức Pythagoras: Trung đoạn = căn bậc hai của (AC^2 - (AC/2)^2) = căn bậc hai của (8^2 - (8/2)^2) = căn bậc hai của (64 - 16) = căn bậc hai của 48 = 4 căn 3 cm
b) Diện tích xung quanh của hình chóp S.ABC là tổng diện tích các mặt bên của hình chóp. Vì tam giác ABC là tam giác đều, nên diện tích mặt bên của hình chóp là diện tích tam giác đều. Ta có công thức tính diện tích tam giác đều: Diện tích tam giác đều = (cạnh^2 * căn 3) / 4 = (8^2 * căn 3) / 4 = 16 căn 3 cm^2
Diện tích xung quanh = Diện tích tam giác đều + Diện tích đáy = 16 căn 3 + 27,72 = 16 căn 3 + 27,72 cm^2
Diện tích toàn phần của hình chóp là tổng diện tích xung quanh và diện tích đáy: Diện tích toàn phần = Diện tích xung quanh + Diện tích đáy = 16 căn 3 + 27,72 + 27,72 = 16 căn 3 + 55,44 cm^2
c) Thể tích của hình chóp tam giác đều S.ABC được tính bằng công thức: Thể tích = (Diện tích đáy * Chiều cao) / 3 = (27,72 * 7,5) / 3 = 69,3 cm^3

Sxq=16*4*17/2=544cm2
Stp=544+16^2=800cm2
V=1/3*16^2*15=1280cm3
Nữa chu vi đáy của hình chóp đều:
\(16\cdot4:2=32\left(cm\right)\)
Diện tích xung quanh của hình chóp đều:
\(S_{xq}=32\cdot17=544\left(cm^2\right)\)
Diện tích mặt đáy của hình chóp đều:
\(S_đ=16^2=256\left(cm^2\right)\)
Diện tích toàn phần của hình chóp đều:
\(S_{tp}=S_đ+S_{xq}=544+256=800\left(cm^2\right)\)
Thể tích của hình chóp đều:
\(V=\dfrac{1}{3}\cdot256\cdot15=1280\left(cm^3\right)\)

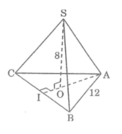
Kẻ AO kéo dài cắt BC tại I
Ta có: AI ⊥ BC (tính chất tam giác đều)
BI = IC = 1/2 BC
Áp dụng định lí pi-ta-go vào tam giác vuông AIB,ta có:
A B 2 = B I 2 + A I 2
Suy ra: A I 2 = A B 2 - B I 2 = 12 2 - 6 2 =108
AI = 108 cm
Vì tam giác ABC đều nên O là trọng tâm của tam giác ABC
Ta có: OI = 1/3.AI = 1/3. 108 cm
Áp dụng định lí pi-ta-go vào tam giác vuông SOI ta có:
S I 2 = S O 2 + O I 2 = 8 + 1/9 .108 = 76
SI = 76 cm
Vậy S x q = Pd= [(12.3):2]. 76 =18 76 cm

a:ΔSBC cân tại S có SM là trung tuyến
nên SM vuông góc BC
BC=6cm
=>BM=CM=3cm
SM=căn 5^2-3^2=4cm
Sxq=5*3/2*4=5*3*2=30cm2
Stp=30+5^2*căn 3/2=(60+25căn 3)/2cm2
b: BC vuông góc SM
BC vuông góc AM
=>BC vuông góc (SAM)

a) Diện tích xung quanh của hình chóp tam giác đều là: \(\frac{{10.3}}{2}.12 = 180\) (\(c{m^2}\))
b) Diện tích xung quanh của hình chóp tứ giác đều là: \(\frac{{72.4}}{2}.77 = 11088\) (\(d{m^2}\))
Diện tích đáy của hình chóp tứ giác đều là: \({72^2}=5184\) (\(d{m^2}\))
Diện tích toàn phần của hình chóp tứ giác đều là: \(11088 + 5184 = 16 272\) (\(d{m^2}\))
Thể tích của hình chóp tứ giác đều là: \(\frac{1}{3}.5184.68,1=117676,8\) (\(d{m^3}\))

Nữa chu vi đáy của hình chóp đều:
\(8\cdot4:2=16\left(cm\right)\)
Diện tích xung quanh của hình chóp đều:
\(S_{xq}=16\cdot5=80\left(cm^2\right)\)
Diện tích đáy của hình chóp đều:
\(S_đ=8^2=64\left(cm^2\right)\)
Diện tích toàn phần của hình chóp đều:
\(S_{tp}=S_đ+S_{xq}=64+80=144\left(cm^2\right)\)

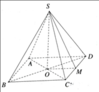

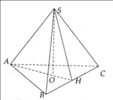


a) Chân đường cao H của hình chóp S.ABC trùng với trọng tâm của tam giác ABC.
Gọi M là trung điểm của BC
Tam giác ABC có
b) Tam giác SAM cân ở M nên
Diện tích xung quanh của hình chóp:
c) Diện tích toàn phần của hình chóp:
d) Thể tích của hình chóp