Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Xét một trường hợp đặc biệt của các điểm M, E, F ta tính được T = 1.

Đáp án là C
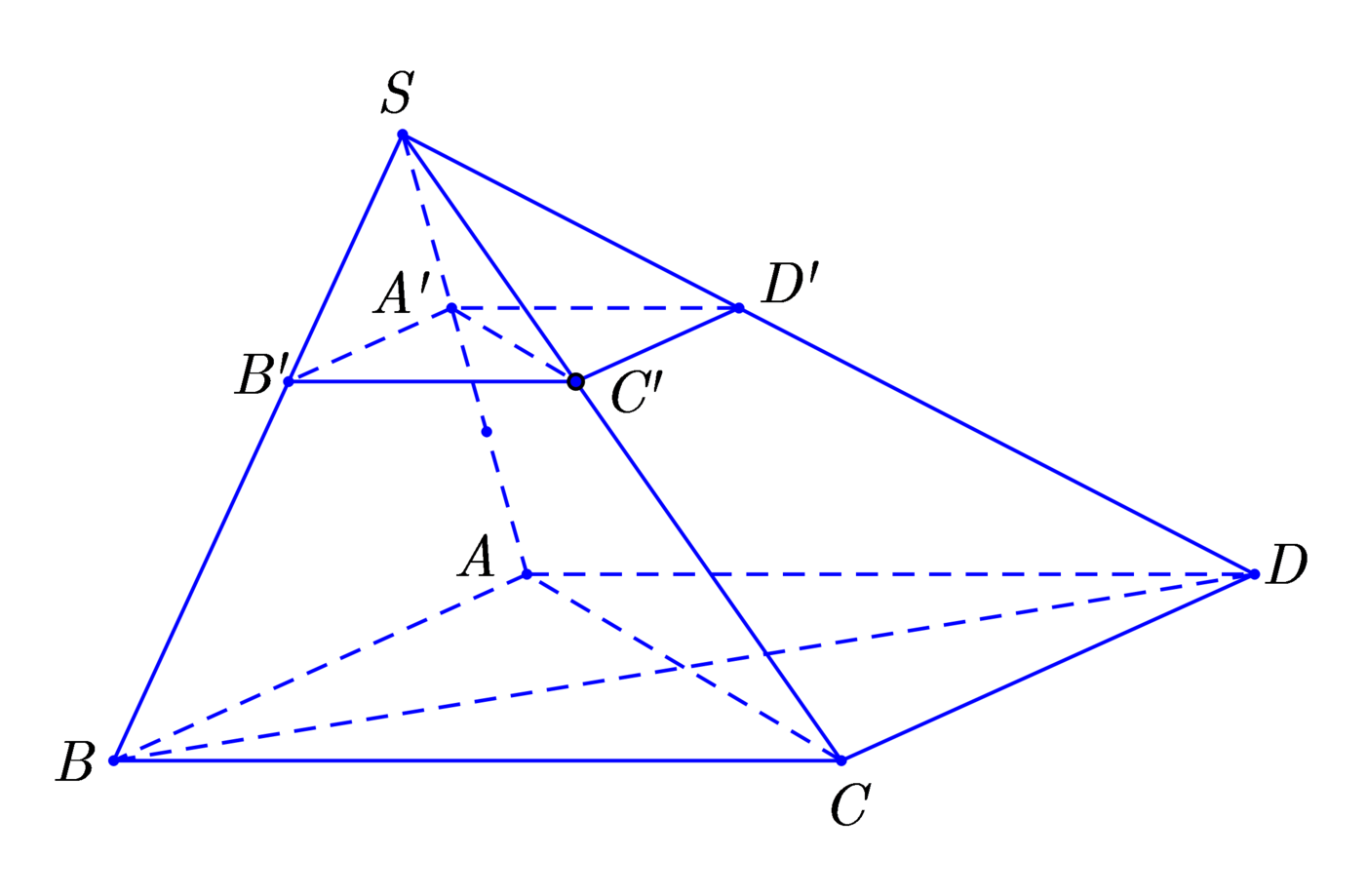
V S . A ' B ' C ' V S . A B C = 1 27 ⇒ V S . A ' B ' C ' = 1 27 V S . A B C ⇒ V S . A B C D = 2 V S . A ' B ' C ' = 2 27 . 1 2 V S . A B C D = V 27 .

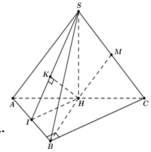
Gọi H là trung điểm của AC
Đỉnh S cách đều các điểm A, B, C ![]()
Xác đinh được ![]()
Ta có MH//SA ![]()
Gọi I là trung điểm của AB ![]()
![]() và chứng minh được
và chứng minh được ![]()
Trong tam giác vuông SHI tính được ![]()
Chọn A.

Đáp án A
Phương pháp giải: Xác định tọa độ ba điểm A, B, C và gọi tâm I, sử dụng điều kiện cách đều IA = IB = IC = IO để tìm tọa độ tâm I của mặt cầu
Lời giải:
Gọi A(a;0;0); B(0;b;0); C(0;0;c) => Tọa độ trọng tâm G là
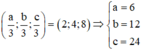
Gọi tâm mặt cầu (S) là
![]()
![]()
![]()
![]()
![]()
Vậy tọa độ tâm mặt cầu là I(3;6;12)
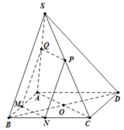
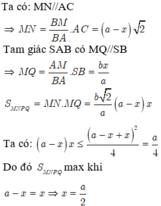

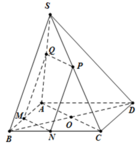
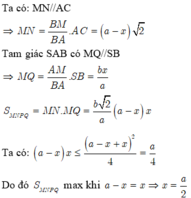
Đáp án C
Gọi M,N,P lần lượt là giao điểm của OA, OB, OC với cạnh BC, CA, AB.
Vì O B ' / / S A ⇒ O A ' S A = O M A M (Định lí Thalet).
Tương tự, ta có O B ' S B = O N B N ' ; O C ' S C = O P P C ⇒ T = O M A M + O N B N + O P P C .
Với O là trọng tâm của tam giác ABC ⇒ M , N , P lần lượt là trung điểm của BC, CA, AB
⇒ O M A M = O N B N = O P C P = 1 3 . Vậy tổng tỉ số T = O A ' S A + O B ' S B + O C ' S C = 1.
Chú ý: Bản chất bài toán là yêu cầu chứng minh O M A M + O N B N + O P P C = 1. Tuy nhiên với tinh thần trắc nghiệm ta sẽ chuẩn hóa với O là trọng tâm tam giác ABC.