K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
9 tháng 10 2019
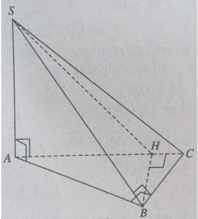
a) BC ⊥ SA & BC ⊥ AB) ⇒ BC ⊥ (SAB)
⇒ BC ⊥ SB.
⇒ tam giác SBC vuông tại B.
b) BH ⊥ AC & BH ⊥ SA ⇒ BC ⊥ (SAC)
⇒ (SBH) ⊥ (SAC).
c) d[B, (SAC)] = BH. Ta có:
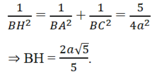

16 tháng 2 2023
a: BC vuông góc SA
BC vuôg góc AB
=>BC vuông góc (SAB)
b: BI vuông góc SA
BI vuông góc AC
=>BI vuông góc (SAC)
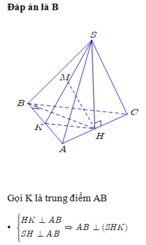
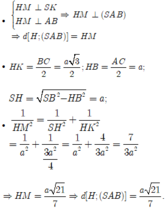

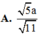
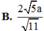
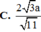
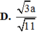

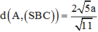

Kẻ \(BK\perp AC\Rightarrow BK\perp\left(SAC\right)\)
\(\Rightarrow BK=d\left(B;\left(SAC\right)\right)\)
\(\dfrac{1}{BK^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow BK=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{a\sqrt{3}}{2}\)
Kẻ \(CP\perp BH\Rightarrow CP\perp\left(SBH\right)\)
\(\Rightarrow CP=d\left(C;\left(SBH\right)\right)\)
\(\widehat{CBP}=\widehat{ACB}=30^0\Rightarrow CH=BC.sin30^0=\dfrac{a\sqrt{3}}{2}\)
\(BH=\dfrac{AC}{2}=\dfrac{1}{2}\sqrt{AB^2+AC^2}=a\)\(\Rightarrow SH=\sqrt{SB^2-BH^2}=a\)
Kẻ \(HE\perp BC\) , kẻ \(HF\perp SE\Rightarrow HF=d\left(H;\left(SBC\right)\right)\)
\(HE=CH.sin30^0=\dfrac{a}{2}\)
\(\dfrac{1}{HF^2}=\dfrac{1}{SH^2}+\dfrac{1}{HE^2}\Rightarrow HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{5}}{5}\)