


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




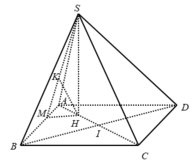
- Ta có: CD // AB nên CD// mp (SAB)
⇒ Suy ra:

- Kẻ MH ⊥ AB, HK ⊥ SM.
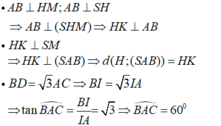
- Do đó, tam giác ABC là tam giác đều.
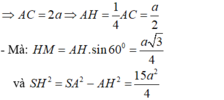
- Xét tam giác SHM vuông tại H; đường cao HK có:
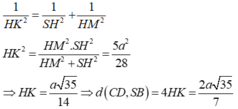

a.
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp AD\\AB\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
Mà \(AD\in\left(SAD\right)\Rightarrow\left(SAD\right)\perp\left(SAB\right)\)
b.
M là điểm nào nhỉ?
c.
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp CD\\HK\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SHK\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SKH}\) là góc giữa (SCD) và (ABCD)
\(HK=AD=a\Rightarrow tan\widehat{SKH}=\dfrac{SH}{HK}=\dfrac{\sqrt{3}}{3}\Rightarrow\widehat{SKH}=30^0\)
d.
Từ H kẻ \(HE\perp SK\) (E thuộc SK)
\(CD\perp\left(SHK\right)\) theo cmt \(\Rightarrow CD\perp HE\)
\(\Rightarrow HE\perp\left(SCD\right)\Rightarrow HE=d\left(H;\left(SCD\right)\right)\)
Hệ thức lượng:
\(\dfrac{1}{HE^2}=\dfrac{1}{SH^2}+\dfrac{1}{HK^2}\Rightarrow HE=\dfrac{a}{2}\)