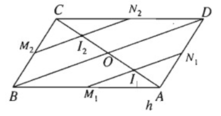
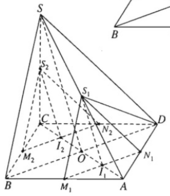
a) Trường hợp 1 .

I thuộc đoạn AO (0 < x < a/2)

Khi đó I ở vị trí I1

Ta có: (α) // (SBD)

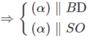
Vì (α) // BD nên (α) cắt (ABD) theo giao tuyến M1N1 ( qua I1) song song với BD

Tương tự (α) // SO nên (α) cắt (SOA) theo giao tuyến

S1T1 song song với SO.

Ta có thiết diện trong trường hợp này là tam giác S1M1N1.

Nhận xét. Dễ thấy rằng S 1 M 1   / /   S B   v à   S 1 N 1   / /   S D . Lúc đó tam giác S1M1N1 đều.

Trường hợp 2. I thuộc đoạn OC (a/2 < x < a)

Khi đó I ở vị trí I2. Tương tự như trường hợp 1 ta có thiết diện là tam giác đều

S 2 M 2 N 2   c ó   M 2 N 2   / /   B D , S 2 M 2   / /   S B ,   S 2 N 2   / /   S D .

Trường hợp 3. I ≡ O. Thiết diện chính là tam giác đều SBD.

b) Ta lần lượt tìm diện tích thiết diện trong các trường hợp 1,2,3.

Trường hợp 1. I thuộc đoạn AO (0 < x < a/2)

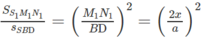
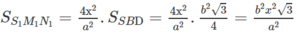
Trường hợp 2. I thuộc đoạn OC (a/2 < x < a)

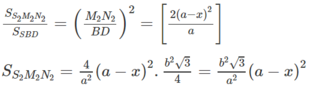
Trường hợp 3. I ≡ O.

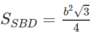
Tóm lại

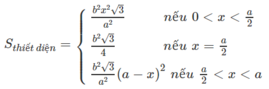
∗ Đồ thị của hàm số S theo biến x như sau:

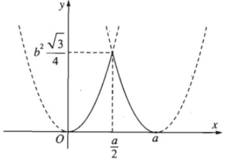
Vậy Sthiết diện lớn nhất khi và chỉ khi x = a/2.

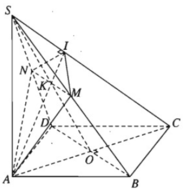
a) Gọi I là giao điểm của mặt phẳng (α) với cạnh SC. Ta có: (α) ⊥ SC, AI ⊂ (α) ⇒ SC ⊥ AI. Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và AI ⊂ (α), nên K là giao điểm của SO với (α).

b) Ta có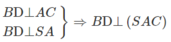 

⇒ BD ⊥ SC

Mặt khác BD ⊂ (SBD) nên (SBD) ⊥ (SAC).

Vì BD ⊥ SC và (α) ⊥ SC nhưng BD không chứa trong (α) nên BD // (α)

Ta có K = SO ∩ (α) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của (α) và (SBD).

Mặt phẳng (SBD) chứa BD // (α) nên cắt theo giao tuyến d // BD. Giao tuyến này đi qua K là điểm chung của (α) và (SBD).

Gọi M và N lần lượt là giao điểm của d với SB và SD. Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.

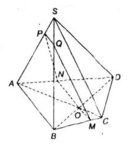
+ Ta có: (α) // AB

⇒ giao tuyến (α) và (ABCD) là đường thẳng qua O và song song với AB.

Qua O kẻ MN // AB (M ∈ BC, N ∈ AD)

⇒ (α) ∩ (ABCD) = MN.

+ (α) // SC

⇒ giao tuyến của (α) và (SBC) là đường thẳng qua M và song song với SC.

Kẻ MQ // SC (Q ∈ SB).

+ (α) // AB

⇒ giao tuyến của (α) và (SAB) là đường thẳng qua Q và song song với AB.

Từ Q kẻ QP // AB (P ∈ SA).

⇒ (α) ∩ (SAD) = PN.

Vậy thiết diện của hình chóp cắt bởi (α) là tứ giác MNPQ.

Ta có: PQ// AB và NM // AB

=> PQ // NM

Do đó, tứ giác MNPQ là hình thang.

Bài này ko hề khó, đầu tiên ta dễ dàng xác định được thiết diện đi qua P theo Talet.

Gọi giao của thiết diện với BC, SD lần lượt là E, F

Để \(PJ||\left(SAD\right)\Rightarrow PJ||ME\Rightarrow PJME\) là hình bình hành (2 cặp cạnh đối song song)

\(\Rightarrow PF=MJ\)

Đến đây sử dụng tỉ lệ tam giác đồng dạng là ra x

Câu b thì từ P kẻ vuông xuống ME và S vuông xuống AB, 2 đường cao này song song theo tỉ lệ tương ứng CP/CS (Talet). Vậy là ra tỉ lệ diện tích

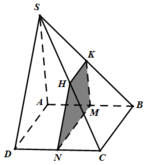
=> giao tuyến của (SCD) và (α) là NH// SD.

+ lại có HK là giao tuyến của (α) và (SBC) .

Thiết diện là tứ giác MNHK.

Ba mặt phẳng (ABCD) ; (SBC) và (α)  đôi một cắt nhau theo các giao tuyến là MN; HK và BC  mà MN// BC nên MN// HK. Vậy thiết diện là một hình thang .

Chọn B.