Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

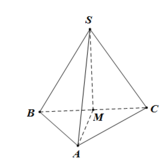
Cho hình chop SABC, có đáy là ABC là tam giác vuông tại B, có độ dài các cạch AB=6,BC=8,SA=10 vuông góc với mặt đáy Tính thể tích khối chóp SABC

Đáp án A
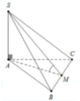
Gọi M là trung điểm của BC, ∆ S B C đều ⇒ S M ⊥ B C
Mà S A ⊥ ( A B C ) ⇒ S A ⊥ B C và S M ⊥ B C suy ra B C ⊥ ( S A M )
Ta có:
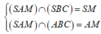
![]()
Xét tam giác SAM vuông tại A có:
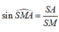
![]()
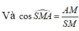
![]()
⇒ S A B C = 1 2 A M . B C = 3 a 2 8
⇒ V S . A B C = 1 3 S A . S A B C = a 3 3 32

hình như đáp số hơi xấu thì phải bạn ạ? :D có gì check lại các phép toán hộ mình nhé
Hình vẽ minh họa và các thao tác vẽ hình ở bên dưới
Dễ tính: \(SK=\sqrt{SB^2-BK^2}=\dfrac{a\sqrt{7}}{6}\)
Ta lại có: \(S_{SAK}=\dfrac{1}{2}SG.AK=\dfrac{1}{2}HK.SA\)
\(\Rightarrow HK=\dfrac{SG.AK}{SA}=\dfrac{a}{3}\) Trong đó: \(SG=\dfrac{a}{3};AK=\dfrac{2a}{3};SA=SB=SC=\dfrac{2a}{3}\) ( Tam giác SAK cân tại A )
\(\Rightarrow SH=\sqrt{SK^2-HK^2}=\dfrac{a\sqrt{3}}{6}\)
Theo định lý Symson: \(\dfrac{S_{SHBC}}{S_{SABC}}=\dfrac{SH}{SA}=\dfrac{\sqrt{3}}{4}\Rightarrow S_{SHBC}=\dfrac{\sqrt{3}}{4}S_{SABC}\) (1)
\(\Rightarrow S_{HABC}=\left(\dfrac{4-\sqrt{3}}{4}\right)S_{SABC}\) (2)
Từ (1) và (2) suy ra được tỉ lệ thể tích giữa 2 phần là: \(\dfrac{3+4\sqrt{3}}{13}\)
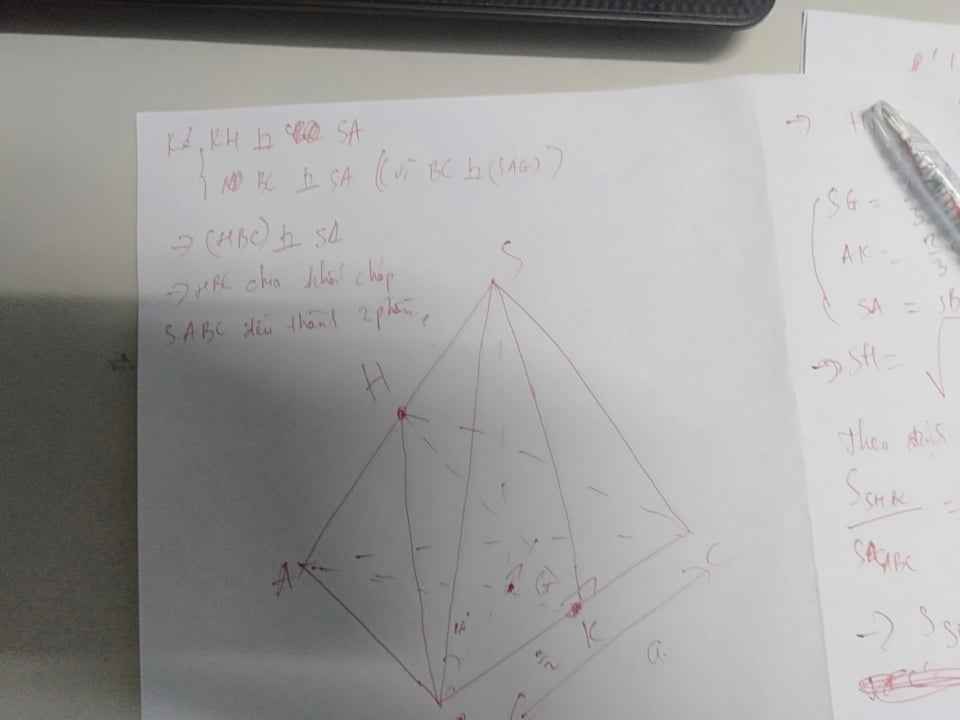

Kiểm tra lại đề bài câu này
Nếu góc giữa SB và đáy là 30 độ thì (P) sẽ cắt SA tại 1 điểm nằm ngoài khối chóp (nằm phía trên điểm S chứ không nằm giữa S và A) nên không thể chia khối chóp thành 2 phần được.
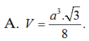
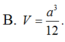

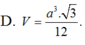
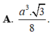
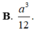
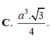
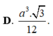
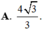
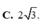
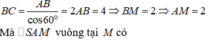
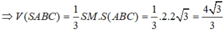
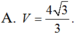

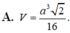
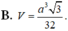
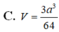
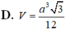

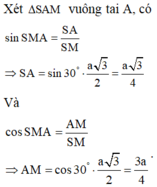
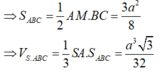
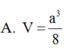
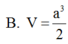

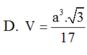
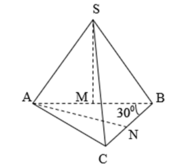
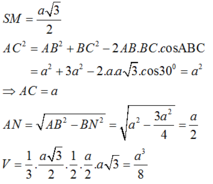
Đáp án A