Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

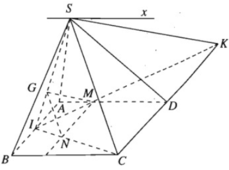
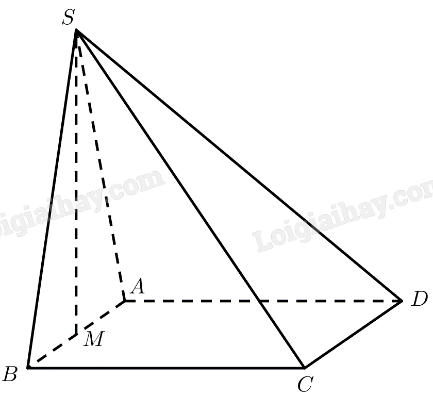
a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có:
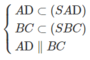
⇒ (SAD) ∩ (SBC) = Sx
Và Sx // AD // BC.
b) Ta có: MN // IA // CD
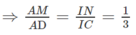
Mà 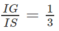
(G là trọng tâm của ∆SAB) nên
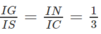 ⇒ GN // SC
⇒ GN // SC
SC ⊂ (SCD) ⇒ GN // (SCD)
c) Giả sử IM cắt CD tại K ⇒ SK ⊂ (SCD)
MN // CD ⇒
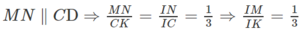
Ta có:
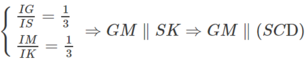

a, Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)
\(\left. \begin{array}{l} \Rightarrow SM \bot AB\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right\} \Rightarrow SM \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình chữ nhật \( \Rightarrow AB \bot A{\rm{D}}\)
\(SM \bot \left( {ABCD} \right) \Rightarrow SM \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)
c) \(A{\rm{D}} \bot \left( {SAB} \right) \Rightarrow A{\rm{D}} \bot SB\)
Tam giác \(SAB\) vuông cân tại \(S\)\( \Rightarrow SA \bot SB\)
\(\left. \begin{array}{l} \Rightarrow SB \bot \left( {SA{\rm{D}}} \right)\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)
Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)
\(\left. \begin{array}{l} \Rightarrow SM \bot AB\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right\} \Rightarrow SM \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình chữ nhật \( \Rightarrow AB \bot A{\rm{D}}\)
\(SM \bot \left( {ABCD} \right) \Rightarrow SM \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)
c) \(A{\rm{D}} \bot \left( {SAB} \right) \Rightarrow A{\rm{D}} \bot SB\)
Tam giác \(SAB\) vuông cân tại \(S\)\( \Rightarrow SA \bot SB\)
\(\left. \begin{array}{l} \Rightarrow SB \bot \left( {SA{\rm{D}}} \right)\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)

a:
b: ABCD là hình chữ nhật
=>AB//CD và BC//AD
BC//AD
\(AD\subset\left(SAD\right)\)
BC không nằm trong mp(SAD)
Do đó: BC//(SAD)
c: AB//CD
\(CD\subset\left(SCD\right)\)
AB không nằm trong mp(SCD)
Do đó: AB//(SCD)
d: Xét ΔSAC có
O,H lần lượt là trung điểm của CA,CS
=>OH là đường trung bình của ΔSAC
=>OH//SA
OH//SA
\(SA\subset\left(SAB\right)\)
OH không nằm trong mp(SAB)
Do đó: OH//(SAB)

a: 
b: BC//AD(ABCD là hình chữ nhật)
\(AD\subset\left(SAD\right)\)
BC không nằm trong mp(SAD)
Do đó: BC//(SAD)
c: AB//CD(ABCD là hình chữ nhật)
\(CD\subset\left(SCD\right)\)
AB không nằm trong mp(SCD)
Do đó: AB//(SCD)
d: Xét ΔSAC có
O,H lần lượt là trung điểm của CA,CS
=>OH là đường trung bình
=>OH//SA
OH//SA
\(SA\subset\left(SAB\right)\)
OH không nằm trong mp(SAB)
Do đó: OH//(SAB)

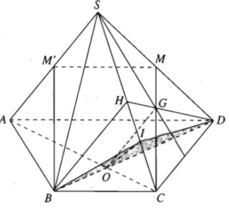
a) Gọi H là trung điểm của SC
Ta có:
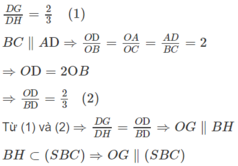
b) Gọi M’ là trung điểm của SA ⇒ MM′ // AD và MM′ = AD/2.
Mặt khác vì BC // AD và BC = AD/2 nên BC // MM′ và BC = MM′.
Do đó tứ giác BCMM’ là hình bình hành ⇒ CM // BM′ mà BM′ ⊂ (SAB)
⇒ CM // (SAB)
c) Ta có: 
Mặt khác vì 
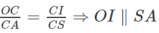
OI ⊂ (BID) ⇒ SA // (BID)

a: Sửa đề; BC vuông góc SB
BC vuông góc AB
BC vuông góc SA
=>BC vuôg góc (SAB)
=>CB vuông góc SB
c: (SO;(SCD))=(SO;SK)=góc KSO(OK vuông góc DC tại K)
\(AO=\dfrac{AC}{2}=1.5a\)
\(SA=\sqrt{SC^2-AC^2}=\sqrt{\left(5a\right)^2-\left(3a\right)^2}=4a\)
\(SO=\sqrt{SA^2+AO^2}=\dfrac{a\sqrt{73}}{2}\)
\(AD=BC=\sqrt{\left(3a\right)^2-a^2}=2a\sqrt{2}\)
Xét ΔACD có
O là trung điểm của AC
OK//AD
=>K là trung điểm của CD
=>DK=CK=a/2
\(AK=\sqrt{\left(2a\sqrt{2}\right)^2+\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{33}}{2}\)
\(SK=\sqrt{SA^2+AK^2}=\sqrt{\left(4a\right)^2+\dfrac{33}{4}a^2}=\dfrac{a\sqrt{97}}{2}\)
OK=AD/2=a căn 2
\(SO=\dfrac{a\sqrt{73}}{2}\)
\(cosKSO=\dfrac{SK^2+SO^2-OK^2}{2\cdot SK\cdot SO}\simeq0.96\)
=>góc KSO=16 độ
Câu c bn ch c/m đc OK vuông góc vs mp (SCD)
Thì sao xác định đc góc cần tìm là OSK

Hình câu c là tui vẽ riêng ra cho dễ nhìn thôi, còn hình vẽ trình bày vô bài lấy hình chung ở câu a và b nhó :v



