Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Tồn tại 5 mặt phẳng thỏa mãn đề bài là:
- Mp đi qua trung điểm AD,BC,SC,SD
- Mp đi qua trung điểm CD,AB,SC,SB
- Mp đi qua trung điểm AD,BC,SB,SA
- Mp đi qua trung điểm CD,AB,SA,SD
- Mp đi qua trung điểm SA,SB,SC,SD

THAM KHẢO:

CD//AB nên góc giữa SB và CD là góc giữa AB và SB, \(\widehat{ABS}\)
CB//AD nên góc giữa SD và CB là góc giữa SD và AD, \(\widehat{ADS}\)
Ta có: tan\(\widehat{ABS}\)=tan\(\widehat{ADS}\)=\(\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
Suy ra \(\widehat{ABS}\)=\(\widehat{ADS}\)=\(\dfrac{\pi}{3}\)

Đáy là hình vuông hay chữ nhật bạn? Hình chữ nhật sao có các cạnh bằng nhau và bằng a được?

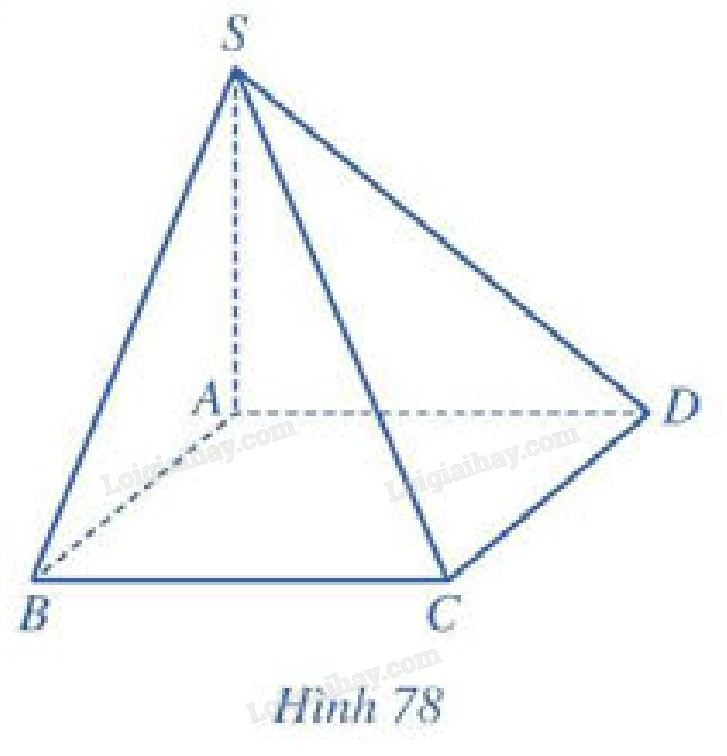
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot C{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{D}} \bot C{\rm{D}}\)
\(\begin{array}{l} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot S{\rm{D}}\\ \Rightarrow d\left( {S,C{\rm{D}}} \right) = S{\rm{D}} = \sqrt {S{A^2} + A{{\rm{D}}^2}} = a\sqrt 2 \end{array}\)
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot A{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{B}} \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SA{\rm{B}}} \right) \Rightarrow d\left( {D,\left( {SAB} \right)} \right) = A{\rm{D}} = a\)
c) Kẻ \(AH \bot S{\rm{D}}\left( {H \in S{\rm{D}}} \right)\).
\(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot AH\)
\( \Rightarrow AH \bot \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = AH\)
Tam giác \(SAD\) vuông tại \(A\) có đường cao \(AH\)
\( \Rightarrow AH = \frac{{SA.A{\rm{D}}}}{{S{\rm{D}}}} = \frac{{a\sqrt 2 }}{2}\)
Vậy \(d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = \frac{{a\sqrt 2 }}{2}\).

a: Chọn mp(ABCD) có chứa CD
Xét ΔSBD có
E,I lần lượt là trung điểm của SB,SD
=>EI là đường trung bình của ΔSBD
=>EI//BD
Xét (ABCD) và (AIE) có
\(A\in\left(ABCD\right)\cap\left(AIE\right)\)
EI//BD
Do đó: (ABCD) giao (AIE)=xy, xy đi qua A và xy//BD//EI
Gọi K là giao điểm của xy với CD
=>K là giao điểm của CD với mp(AIE)
a: Chọn mp(ABCD) có chứa CD
Xét ΔSBD có
E,I lần lượt là trung điểm của SB,SD
=>EI là đường trung bình của ΔSBD
=>EI//BD
Xét (ABCD) và (AIE) có
EI//BD
Do đó: (ABCD) giao (AIE)=xy, xy đi qua A và xy//BD//EI
Gọi K là giao điểm của xy với CD
=>K là giao điểm của CD với mp(AIE)

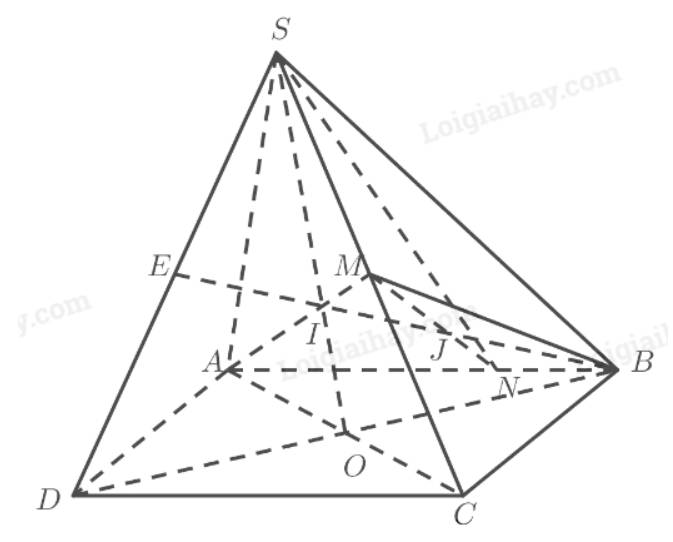
a) Gọi \(O\) là giao điểm của \(AC\) và \(BD\), \(I\) là giao điểm của \(AM\) và \(SO\). Ta có:
\(\left. \begin{array}{l}I \in SO \subset \left( {SB{\rm{D}}} \right)\\I \in AM\end{array} \right\} \Rightarrow I = AM \cap \left( {SB{\rm{D}}} \right)\)
Xét tam giác \(SAC\) có:
\(ABCD\) là hình bình hành \( \Rightarrow O\) là trung điểm của \(AC\)
Theo đề bài ta có \(M\) là trung điểm của \(SC\)
Mà \(I = SO \cap AM\)
\( \Rightarrow I\) là trọng tâm của .
b) Gọi \(E\) là giao điểm của \(S{\rm{D}}\) và \(BI\). Ta có:
\(\left. \begin{array}{l}E \in BI \subset \left( {ABM} \right)\\E \in S{\rm{D}}\end{array} \right\} \Rightarrow E = S{\rm{D}} \cap \left( {ABM} \right)\)
c) Gọi \(J\) là giao điểm của \(MN\) và \(BE\). Ta có:
\(\left. \begin{array}{l}J \in BE \subset \left( {SB{\rm{D}}} \right)\\J \in MN\end{array} \right\} \Rightarrow J = MN \cap \left( {SB{\rm{D}}} \right)\)

a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
b: AC vuông góc BD
BD vuông góc SO
=>BD vuông góc (SAC)
=>(SBD) vuông goc (SAC)
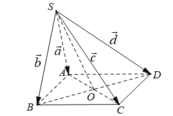
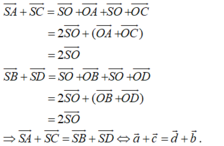
- Gọi O là tâm của hình bình hành ABCD. Ta có:
- Từ (1) và (2) suy ra: