Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Trong mp (ABCD), nối AN kéo dài cắt BC kéo dài tại E
⇒E∈(SBC)⇒E∈(SBC)
Do AD song song BE, áp dụng Talet:
ANNE=NDNC=1⇒AN=NE⇒ANNE=NDNC=1⇒AN=NE⇒ N là trung điểm AE
⇒MN⇒MN là đường trung bình tam giác SAE
⇒MN//SE⇒MN//(SBC)
Đề bài sai òi :v Vẽ hình ra đi bạn.
Giờ tui gán MN vô (SBD) thì giao tuyến của (SBD) và (SBC) là SB. Vậy nên SB phải song song với MN. Nhưng ko :) Song song chết liền hà :)
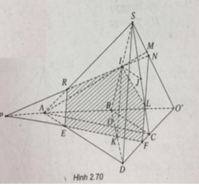
a) Gọi O′ = AB ∩ CD, M = AI ∩ SO′
Ta có: M = AI ∩ (SCD)
b) IJ // BC ⇒ IJ // AD ⇒ IJ // (SAD)
c) Đường thẳng qua I song song với SD cắt BD tại K.
Do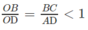 
nên OB < OD. Do đó điểm K thuộc đoạn OD.
Qua K, kẻ đường thẳng song song với AC cắt DA, DC, BA lần lượt tại E, F, P.
Gọi R = IP ∩ SA. Kéo dài PI cắt SO’ tại N
Gọi L = NF ∩ SC
Ta có thiết diện là ngũ giác IREFL.
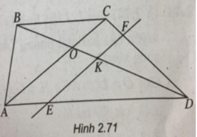
a: BD giao AC tại O
S thuộc (SBD) giao (SAC)
=>(SBD) giao (SAC)=SO
Gọi giao của SO và KH là G
\(\left\{{}\begin{matrix}G\in KH\subset\left(KHC\right)\\G\in SO\subset\left(SAC\right)\end{matrix}\right.\)
\(\left\{{}\begin{matrix}C\in\left(KHC\right)\\C\in\left(SAC\right)\end{matrix}\right.\)
=>(KHC) giao (SAC)=CG
b: Chọn mp (SAC) có chứa SA
(SAC) giao (KHC)=CG
=>I=SA giao CG
c: Chọn mp (ABCD) có chứa AB
(ABCD) cắt (KHC)=HC
=>E=AB giao HC
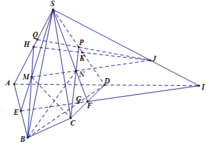
a) Do MN\(\subset\) (BMN); AD \(\subset\)(ABCD) nên I là một điểm chung của (BMN) với (ABCD). Dễ thấy B là một điểm chung khác I
Vậy (BMN)\(\cap\) (ABCD) =BI
b) J\(\in\)BI\(\subset\) (BMN)
J \(\in\) (CD) \(\subset\) (SCD)
nên J là một điểm chung của (BMN) \(\cap\) (SCD)
vậy (SCD) \(\cap\) (BMN) =NJ
Thiết diện của (BMN) với hình chóp là tứ giác AMNJ
c) Áp dụng định lí Menelaus Trong \(\Delta SAD\) có cát tuyến MNI có:
\(\dfrac{ID}{IA}.\dfrac{MA}{MS}.\dfrac{NS}{ND}=1\)
\(\dfrac{ID}{IA}.1.2=1\) => \(\dfrac{ID}{IA}=\dfrac{1}{2}\)
=> D là trung điểm AI
+ Xét tam giác SAI có 2 trung tuyến MI, SD giao nhau tại N => N là trong tâm tam giác SAI
=> \(\dfrac{NI}{MI}=\dfrac{2}{3}\)
Ta có AD//BC
=> \(\dfrac{IK}{BK}=\dfrac{AI}{BC}=\dfrac{2AD}{BC}=2\)(do AD=BC)
=> \(\dfrac{IK}{IB}=\dfrac{2}{3}\)
Xét tam giác MIB có: \(\dfrac{NI}{MI}=\dfrac{IK}{IB}=\dfrac{2}{3}\)
=> BM//NK