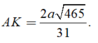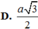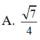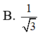Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Lời giải. Để cho gọn ta chọn a=1
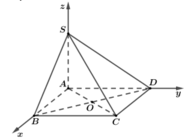
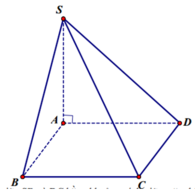
Chọn hệ trục tọa độ Oxyz như hình vẽ với A(0;0;0) và B(1;0;0) , D(0; 3 ;0)
Suy ra C(1; 3 ;0)
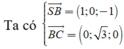
VTPT của mặt phẳng (SBC) là
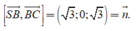
Đường thẳng có VTCP là
![]()
Khi đó
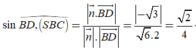
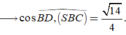

Chọn đáp án A
+ Ta có
![]()
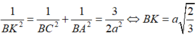
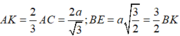
nên K là trọng tâm của tam giác BCD
+ Ta dễ dàng chứng minh được SH ⊥ (BKH) ⇒ SB, (BKH) = SBH
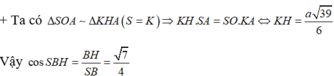

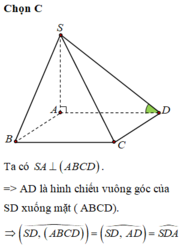
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(\Rightarrow\widehat{SBA}=45^0\Rightarrow SA=AB.tan45^0=a\)
Gọi O là tâm đáy \(\Rightarrow AO=CO\Rightarrow d\left(C;\left(SBD\right)\right)=d\left(A;\left(SBD\right)\right)\)
Kẻ AH vuông góc BD, kẻ AK vuông góc SH
\(\Rightarrow AK\perp\left(SBD\right)\Rightarrow AK=d\left(A;\left(SBD\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AD^2}+\dfrac{1}{AB^2}=\dfrac{1}{a^2}+\dfrac{1}{4a^2}=\dfrac{5}{4a^2}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{SA^2}+\dfrac{1}{AK^2}=\dfrac{1}{a^2}+\dfrac{5}{4a^2}=\dfrac{9}{4a^2}\)
\(\Rightarrow AK=\dfrac{2a}{3}\Rightarrow d\left(C;\left(SBD\right)\right)=\dfrac{2a}{3}\)

Chọn A.

Xác định được
![]()
Vì M là trung điểm SA nên
![]()
Kẻ AK ⊥ DM và chứng minh được AK ⊥ (CDM) nên
![]()
Trong tam giác vuông MAD tính được