Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
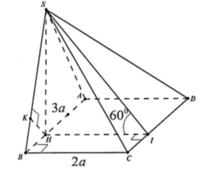
Do $SA\perp (ABCD)$ nên $\angle (SB, ABCD)=\angle (SB, AB)=\widehat{SBA}=45^0$
$\Rightarrow SAB$ là tam giác vuông cân tại $A$
$\Rightarrow SA=AB=a$
Áp dụng định lý Pitago: $SD=\sqrt{SA^2+AD^2}=\sqrt{a^2+(2a)^2}=\sqrt{5}a$

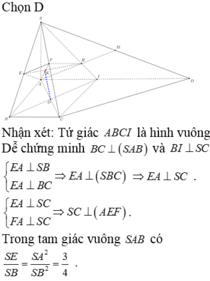
Chọn đáp án D.
Ta có: ![]()
Kẻ 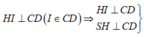
![]()
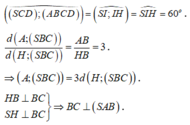
Kẻ ![]()
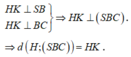
Xét tam giác SHI vuông tại H:
![]()
![]()
Xét tam giác SHB vuông tại B: 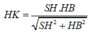
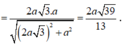
![]()
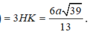

Do H là trung điểm của AB,
=> SH vuông (ABCD)
Do đó SH vuông HD. Có \(SH=\sqrt{SD^2-DH^2}=\sqrt{SD^2-\left(AH^2+AD^2\right)}=a\)
\(\Rightarrow V_{S.ABCD}=\frac{1}{3}S.H.S_{ABCD}=\frac{a^3}{3}\)
Gọi K là hình chiếu vuông góc với H trên BD vs2 E là là hình chiếu vuông góc của H trên SK.
Có : BD vuông HK, BD vuông SH, BD vuông (SHK)
=> BD vuông HE.
Mà HE vuông SK
Do đó HE vuông (SBD)
Ta có : HK = HB \(\sin\widehat{KBH}=\frac{a\sqrt{2}}{4}\)
=> HE = \(\frac{HS.HK}{\sqrt{HS^2+HK^2}}=\frac{4}{3}\)
Do đó, d (A,(SBD)) = 2d (H,(SBD)) = 2HE = 2a/3

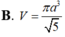



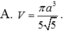


Câu hỏi của Nguyễn Bình Nguyên - Toán lớp 12 | Học trực tuyến
@@ 2 bài đâu giống nhau đâu bạn @@