Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Phương pháp:
- Chứng minh tứ giác AEFH nội tiếp, từ đó tìm tâm đường tròn ngoại tiếp tam giác EHF .
- Tìm đỉnh hình nón và tính chiều cao, bán kính đáy rồi suy ra thể tích.
Cách giải:
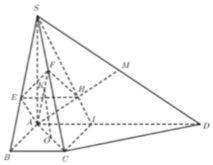




Ta có A là điểm chung thứ nhất.
Gọi 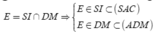
=> E là điểm chung thứ hai.
Vậy AE là giao tuyến của (ADM) và (SAC)
Chọn B.

Đáp án B
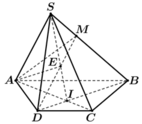
Gọi O là tâm hình bình hành ABCD suy ra O ∈ M N và O ∈ A C
Vậy S M N ∩ S A C = S O

Đáp án C

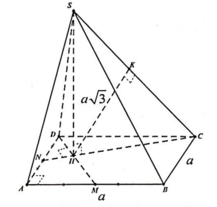
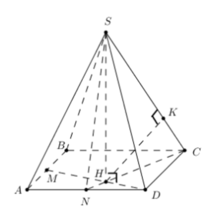
Rễ thấy Δ C D N = Δ D A M ⇒ D C N ^ = A D M ^
mà C D H ^ + M D H ^ = 90 0 ⇒ C D H ^ + D C H ^ = 90 0 ⇒ C H ⊥ D H
mà C H ⊥ S H do S H ⊥ A B C D ⇒ D H ⊥ S C H .
Như vậy kẻ H K ⊥ S C thì HK là đường vuông góc chung của DM và SC hay HK là khoảng cách cần xác định.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
C D 2 = C H . C N ⇒ C H = C D 2 C N = C D 2 C D 2 + D N 2 = 4 a 2 4 a 2 + a 2 = 2 a 5
1 H K 2 = 1 S H 2 + 1 C H 2 = 1 9 a 2 + 5 16 s 2 = 61 144 a 2 ⇒ H K = 12 a 61 61

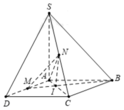
Đáp án A
Vì A M / / B C ⇒ I M I B = M A B C = 1 2 ⇒ d I ; A D d B ; A D = 1 3
|
Suy ra S Δ I M A = 1 2 d I ; A D . A M = 1 2 . 1 3 d B ; A D . 1 2 A D = S A B C D 12
Mà N là trung điểm của S C ⇒ d N ; A B C D = 1 2 d S ; A B C D
Vậy V A M N I V S . A B C D = d N ; A B C D d S ; A B C D . S Δ I M A S A B C D = 1 2 . 1 12 = 1 24


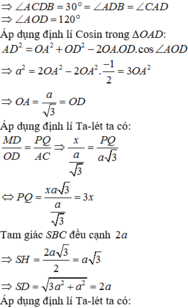




Đáp án C
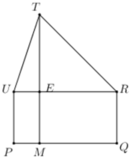
Dễ thấy các cặp đường thẳng BC và AM, BC và SD, BC và DM là các cặp đường thẳng chéo nhau nên chúng không cắt nhau. Theo giả thiết, BC và AD cắt nhau. Ta gọi F là giao điểm của BC và AD.
Do F ∈ A D nên F ∈ A D M , từ đó suy ra F là giao điểm của đường thẳng BC và mặt phẳng (ADM).