K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
29 tháng 11 2018
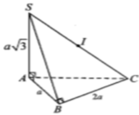
Đáp án A
Phương pháp:
Sử dụng phương pháp tọa độ hóa.
Cách giải:
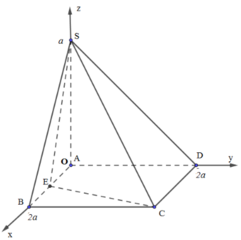
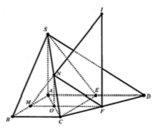
Gắn hệ trục tọa độ như hình vẽ.
Trong đó, B(2a;0;0), C(2a;2a;0), E(a;0;0), S(0;0;a)
Gọi I(x0;y0;z0) là tâm của mặt cầu ngoại tiếp hình chóp S.BEC. Khi đó, IS2 = IB2 = IC2 = IE2
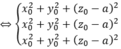
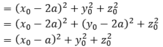
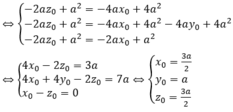
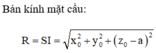
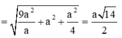
![]()

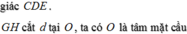
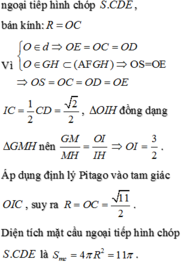
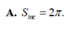
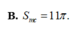


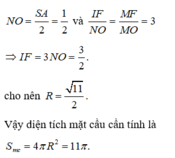
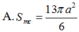

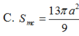
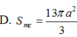
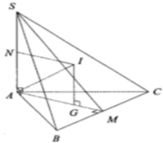

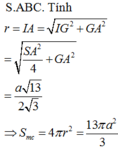

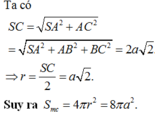
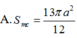
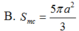
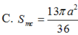
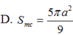
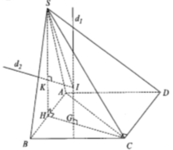

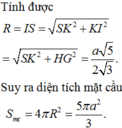
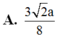
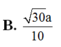
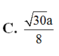
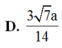
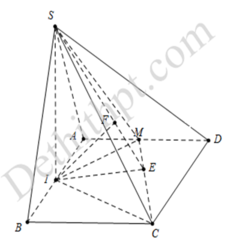
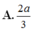

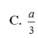
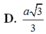
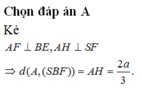


Giải
đàu tiên ta tìm bán kính đường tròn ngoại tiếp tam giác cân ABE (EA=EB)
R=\( \frac{AE.EB.AB}{4S}\) =\(\frac{5}{8}\) .Gọi I là tâm đường trong ngoại tiếp→AI=\(\frac{5}{8}\) .Gọi N là trung điểm SA
Trong mp(SAI) từ I kẻ đt d vuông góc vs đáy.Từ N kẻ đt vuông góc SA cắt d tại O
suy ra O là tâm mặt cầu cần tìm
dựa vào tam giác vuông OAI suy ra bán kính mặt cầu =\(\sqrt{OI^2 +AI^2}\)=\(\frac{\sqrt{41}}{8}\)
suy ra diện tích mặt cầu=4π\(R^2\) suy ra C
theo mình là đáp án C