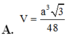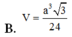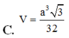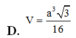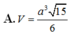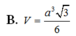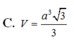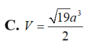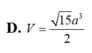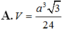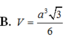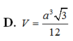K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
29 tháng 4 2018
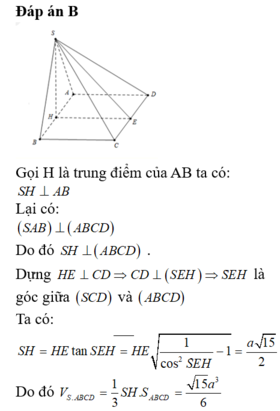
Đáp án B
Phương pháp:
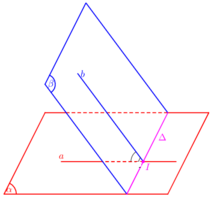
Xác định góc giữa hai mặt phẳng (α;β)
- Tìm giao tuyến Δ của (α;β)
- Xác định 1 mặt phẳng γ ⊥ Δ
- Tìm các giao tuyến a = α∩γ, b = β ∩ γ
- Góc giữa hai mặt phẳng (α;β):(α;β) = (a;b)
Cách giải:
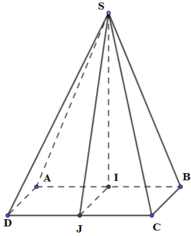
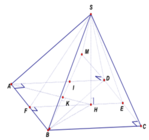
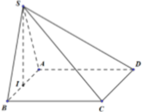
Gọi I, J lần lượt là trung điểm của AB, CD.
Tam giác SAB cân tại S ⇒ SI ⊥ AB
Vì mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD) nên SI ⊥ (ABCD)
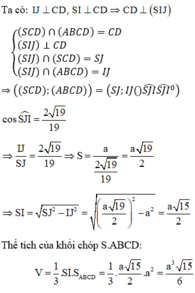

CM
10 tháng 9 2018
Chọn D
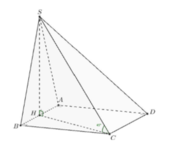
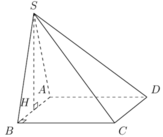
Gọi H là trung điểm của AB.
![]()
![]()
Do đó:
![]()
Xét tam giác vuông BHC:
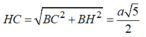
Xét tam giác vuông SHC:
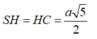
Suy ra:
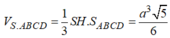

CM
28 tháng 9 2019
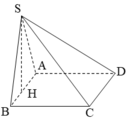
Gọi O là giao điểm của AC và BD.
ABCD là hình thoi ⇒ AC ⊥ BD,
Vì O là trung điểm của AC, BD nên: