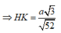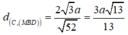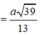Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Do SAB là tam giác đều \(\Rightarrow SH\perp AB\)
Mà \(\left\{{}\begin{matrix}\left(SAB\right)\perp\left(ABCD\right)\\AB=\left(SAB\right)\cap\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SH\perp\left(ABCD\right)\)
Gọi E là trung điểm CD, từ H kẻ \(HF\perp SE\) (F thuộc SE)
\(\left\{{}\begin{matrix}HE\perp CD\\SH\perp\left(ABCD\right)\Rightarrow SH\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SHE\right)\)
\(\Rightarrow CD\perp HF\)
\(\Rightarrow HF\perp\left(SCD\right)\Rightarrow HF=d\left(H;\left(SCD\right)\right)\)
\(HE=BC=a\) ; \(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
Hệ thức lượng:
\(HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{21}}{7}\)
Đáp án B.
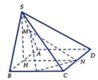
Gọi H là trung điểm của cạnh AB. Khi đó SH ⊥ (ABCD)
Ta có SH ⊥ AB; AB ⊥ HN; HN ⊥ SH và SH = 3
Chọn hệ trục tọa độ Oxyz sao cho H trùng với O, B thuộc tia Ox, N thuộc tia Oy và S thuộc tia Oz. Khi đó: B(1;0;0), A(-1;0;0), N(0;2 3 ;0), C(1;2 3 ;0)
D(-1;2 3 ;0), S(0;0; 3 ), M( - 1 2 ; 0 ; 3 2 ), P(1; 3 ;0)
Mặt phẳng (SCD) nhận
làm một vectơ pháp tuyến; mặt phẳng (MNP) nhận
làm một vectơ pháp tuyến.
Gọi φ là góc tạo bởi hai mặt phẳng (MNP) và (SCD) thì
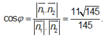
Phân tích phương án nhiễu.
Phương án A: Sai do HS tính đúng
nhưng lại tính sai 
Do đó tính được
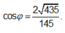
Phương án B: Sai do HS tính đúng 
nhưng lại tính sai
Do đó tính được
Phương án C: Sai do HS tính đúng 
nhưng lại tính sai
Do đó tính được 
Đáp án B.
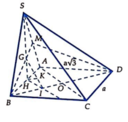
Gọi H là trung điểm AB, G là trọng tâm
Trong mặt phẳng (ABCD), 
Ta có: 
Gọi I là hình chiếu của H lên BD, K là hình chiếu của H lên GI
Ta có: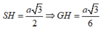 
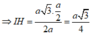
