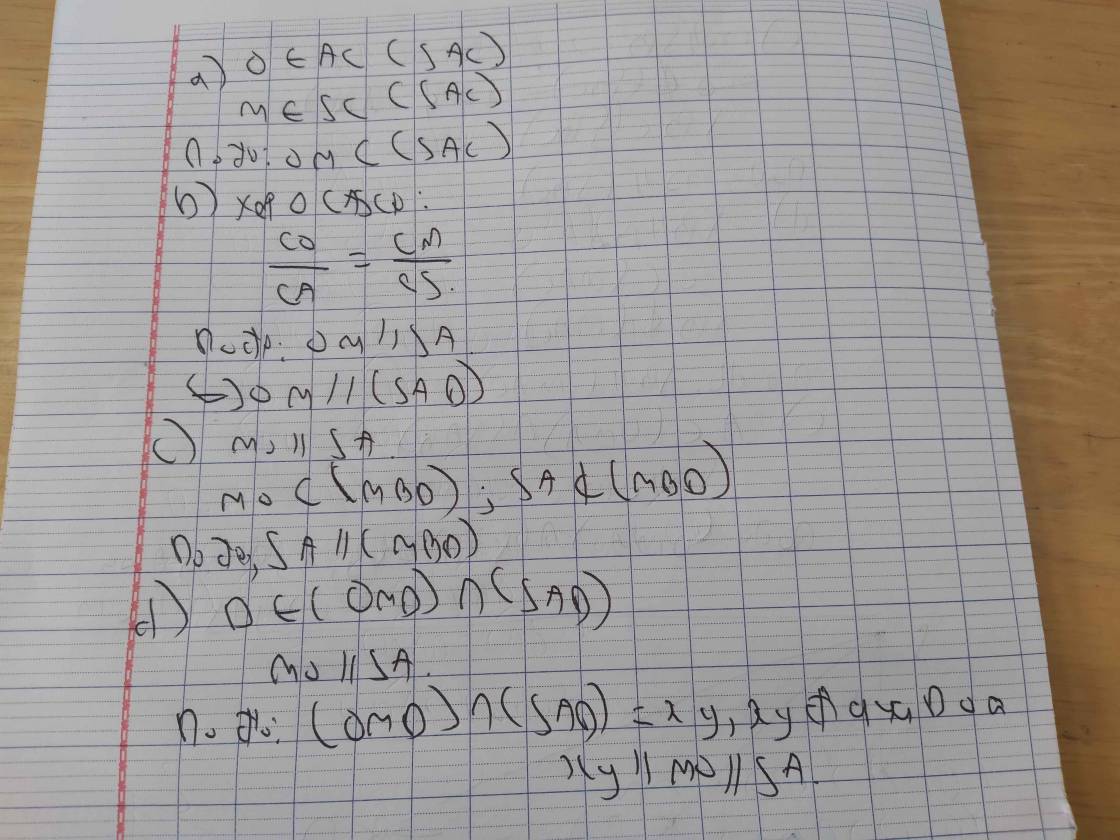Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
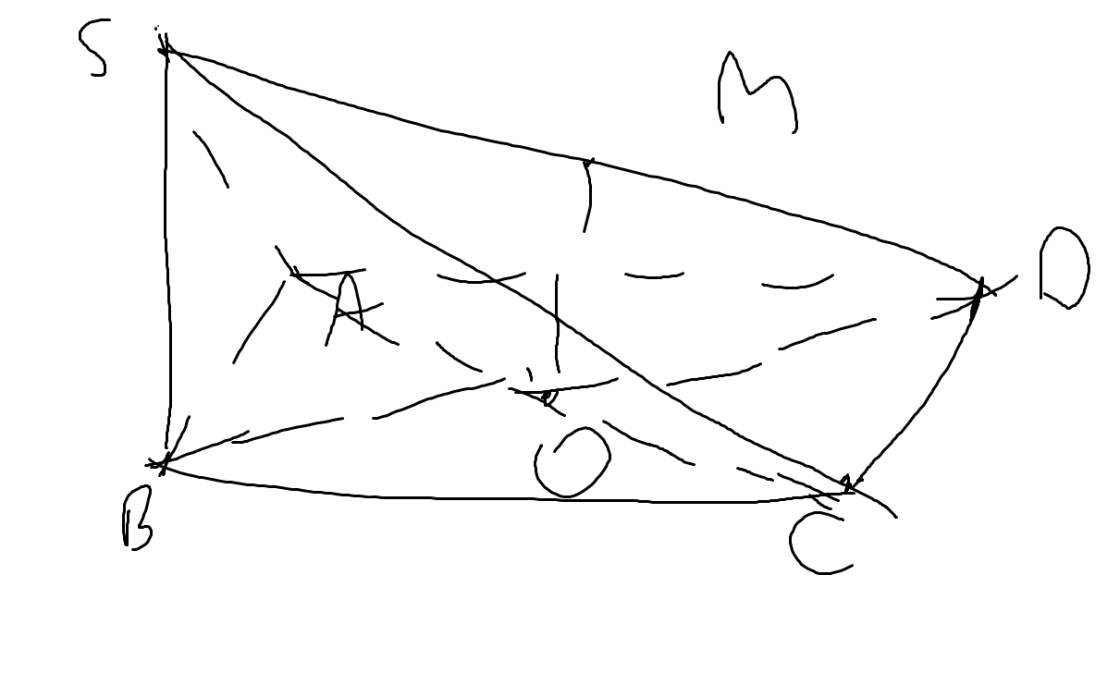
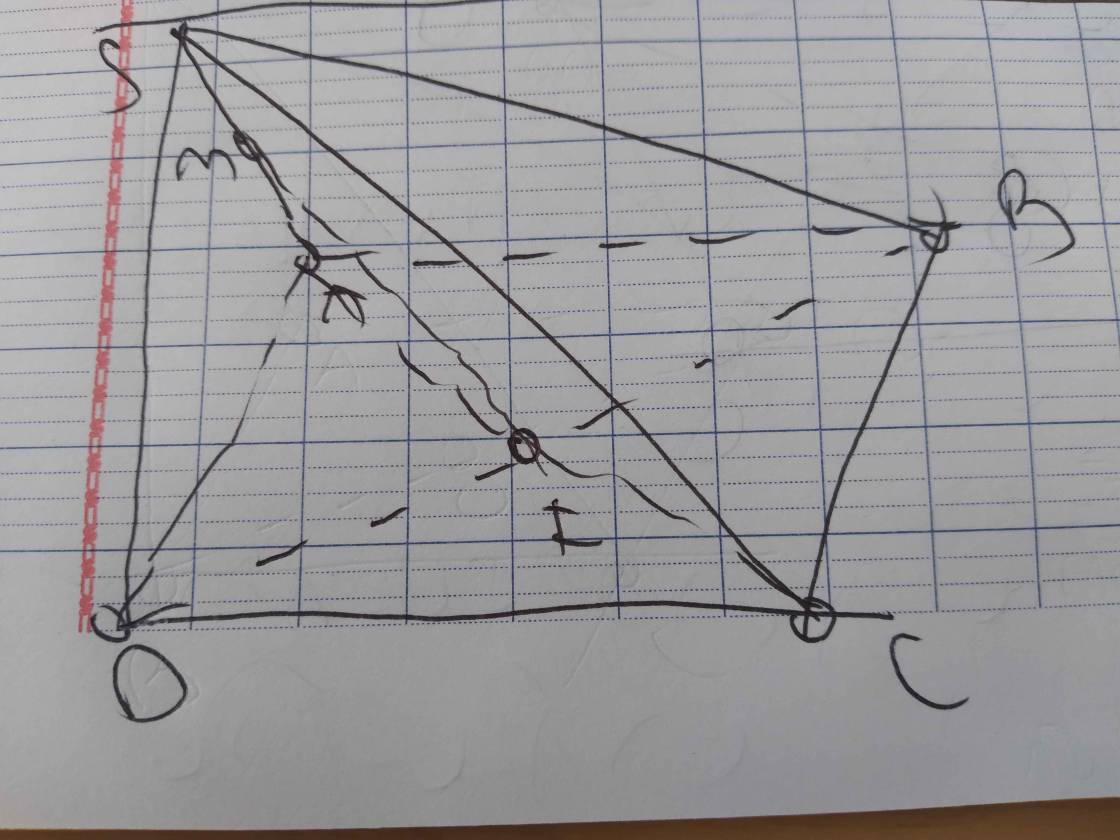
b: \(O\in BD\subset\left(SBD\right);M\in SD\subset\left(SBD\right)\)
=>\(OM\subset\left(SBD\right)\)
c: Xét ΔDSB có
O,M lần lượt là trung điểm của DB,DS
=>OM là đường trung bình của ΔSDB
=>OM//SB
OM//SB
\(SB\subset\left(SBA\right)\)
OM không nằm trong mp(SBA)
Do đó: OM//(SBA)
d: OM//SB
\(SB\subset\left(SBC\right)\)
OM không nằm trong(SBC)
Do đó: OM//(SBC)
e: SB//MO
\(MO\subset\left(MAC\right)\)
SB không nằm trong mp(AMC)
Do đó: SB//(MAC)
f: Xét (OMA) và (SAB) có
\(A\in\left(OMA\right)\cap\left(SAB\right)\)
OM//SB
Do đó: (OMA) giao (SAB)=xy, xy đi qua A và xy//OM//SB

a: XétΔSDB có
M,O lần lượt là trung điểm của DS,DB
=>MO là đường trung bình của ΔSDB
=>MO//SB
SB//MO
MO\(\subset\)(MAC)
SB không nằm trong mp(MAC)
Do đó: SB//(MAC)
b: Xét (OMA) và (SAB) có
\(A\in\left(OMA\right)\cap\left(SAB\right)\)
OM//SB
Do đó: (OMA) giao (SAB)=xy,xy đi qua A và xy//OM//SB

a: 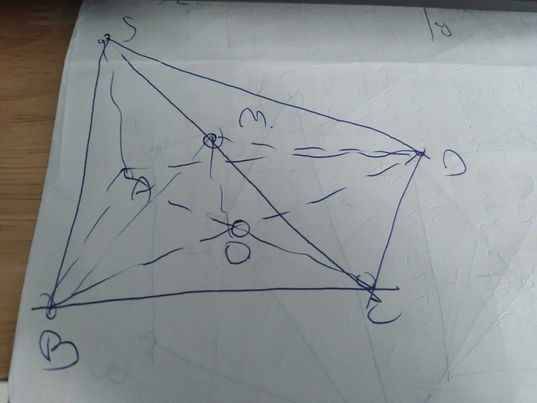
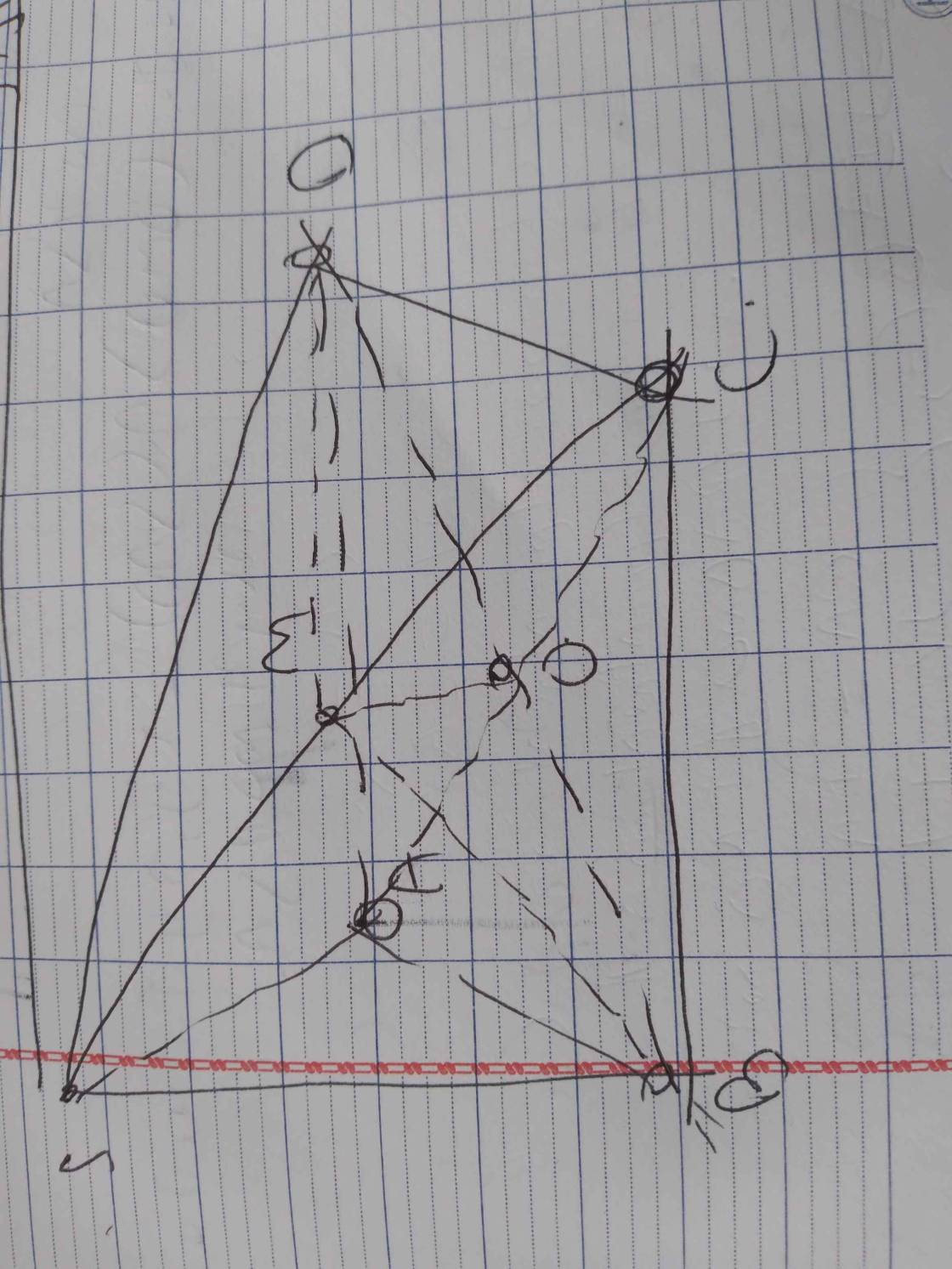
b: \(O\in AC\subset\left(SAC\right);M\in SC\subset\left(SAC\right)\)
Do đó: \(OM\subset\left(SAC\right)\)
c: Xét ΔCAS có
O,M lần lượt là trung điểm của CA,CS
=>OM là đường trung bình
=>OM//SA và OM=SA/2
OM//SA
\(SA\subset\left(SAD\right)\)
OM không nằm trong mp(SAD)
Do đó: OM//(SAD)
d: SA//MO
\(MO\subset\left(MBD\right)\)
SA không nằm trong mp(MBD)
Do đó: SA//(MBD)
e: Xét (OMD) và (SAD) có
OM//SA
\(D\in\left(OMD\right)\cap\left(SAD\right)\)
Do đó: (OMD) giao (SAD)=xy, xy đi qua D và xy//OM//SA

a:
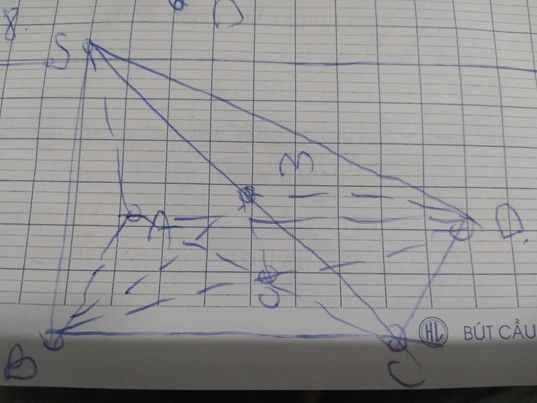
b: \(O\in AC\subset\left(SAC\right)\)
\(M\in SC\subset\left(SAC\right)\)
Do đó: \(OM\subset\left(SAC\right)\)
c: Xét ΔSAC có
O,M lần lượt là trung điểm của CA,CS
=>OM là đường trung bình của ΔSAC
=>OM//SA và \(OM=\dfrac{1}{2}SA\)
OM//SA
SA\(\subset\left(SAD\right)\)
OM không thuộc mp(SAD)
Do đó: OM//(SAD)
d: SA//MO
\(MO\subset\left(MBD\right)\)
SA không thuộc mp(MBD)
Do đó: SA//(MBD)
e: Xét (OMD) và (SAD) có
\(D\in\left(OMD\right)\cap\left(SAD\right)\)
OM//SA
Do đó: \(\left(OMD\right)\cap\left(SAD\right)=xy,D\in xy\) và xy//OM//SA

a: 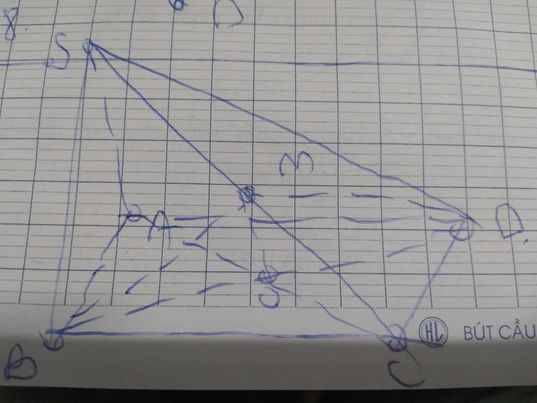
b: \(O\in AC\subset\left(SAC\right)\)
\(M\in SC\subset\left(SAC\right)\)
Do đó: \(OM\subset\left(SAC\right)\)
c: Xét ΔSAC có
O,M lần lượt là trung điểm của CA,CS
=>OM là đường trung bình của ΔSAC
=>OM//SA và \(OM=\dfrac{1}{2}SA\)
OM//SA
SA\(\subset\left(SAD\right)\)
OM không thuộc mp(SAD)
Do đó: OM//(SAD)
d: SA//MO
\(MO\subset\left(MBD\right)\)
SA không thuộc mp(MBD)
Do đó: SA//(MBD)
e: Xét (OMD) và (SAD) có
\(D\in\left(OMD\right)\cap\left(SAD\right)\)
OM//SA
Do đó: \(\left(OMD\right)\cap\left(SAD\right)=xy,D\in xy\) và xy//OM//SA