Trong (SAD) do \(\dfrac{SM}{SA}\ne\dfrac{SP}{SD}\left(\dfrac{1}{2}\ne\dfrac{3}{4}\right)\) nên MP không song song với AD

⇒ Giả sửa MP cắt AD tai E

⇒ E ∈ (ABCD)

Trong (ABCD) gọi K là giao điểm của EN và BC

Trong (ABCD) gọi O là giao điểm của AC và BD

⇒ SO ⊂ (SBD)

Gọi giao điểm của NK và AC là I

Trong (SAC) IM cắt SO tại H

Trong (SBD) DH cắt SB tại Q

⇒ Bla bla bla gì đó

⇒ Thiết diện cần tìm là ngũ giác MPNKQ

Lời giải:

Gọi $Q$ là điểm nằm trên $DC$ sao cho $AD\parallel PQ$

Khi đó: $MN\parallel AD\parallel PQ$ nên $Q\in (MNP)$

$(MNPQ)$ chính là thiết diện của hình chóp cắt bởi $(MNP)$
Giờ ta cần tìm diện tích hình thang $MNPQ$

$SA=SD; DB=SC; AB=CD$ nên $\triangle SAB=\triangle SDC$

Tương ứng ta có $MP=NQ$

$MN=\frac{AD}{2}=\frac{3a}{2}$

$PQ=AD=3a$

$\Rightarrow MNPQ$ là hình thang cân.

Áp dụng định lý cos:

$\cos \widehat{SAB}=\frac{SA^2+AB^2-SB^2}{2SA.AB}=\frac{MA^2+AP^2-MP^2}{2MA.AP}$

$\Leftrightarrow \frac{9a^2+9a^2-27a^2}{2.3a.3a}=\frac{\frac{9}{4}a^2+4a^2-MP^2}{2.\frac{3}{2}a.2a}$

$\Rightarrow MP^2=\frac{37}{4}a^2$

$\Rightarrow h_{MNPQ}=\sqrt{MP^2-(\frac{PQ-MN}{2})^2}=\frac{\sqrt{139}}{4}a$

Diện tích thiết diện:

$S=\frac{MN+PQ}{2}.h=\frac{9\sqrt{139}}{16}a^2$

Kẻ SO vuông góc (ABCD)

\(AM\subset\left(P\right)\)trong mp(SAC)

Gọi AM giao SD=I

Trong mp(SBD) qua I kẻ đường song song với BD cắt SB tại F, cắt SD tại E

=>Thiết diện cần tìm là tứ giác AEMF

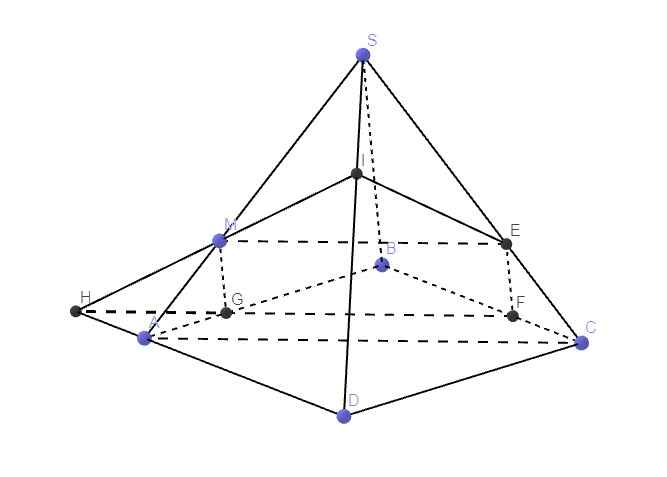
Trong mp (SAB), qua M kẻ đường thẳng song song SB cắt AB tại G \(\Rightarrow G\in\left(P\right)\)

Trong mp (SAC), qua M kẻ đường thẳng song song AC cắt SC tại E \(\Rightarrow E\in\left(P\right)\)

Trong mp (ABCD), qua G kẻ đường thẳng song song AC, lần lượt cắt BC tại F và AD kéo dài tại H

\(\Rightarrow F;H\in\left(P\right)\)

Trong mp (SAD), nối HM kéo dài cắt SD tại I

\(\Rightarrow\) Ngũ giác EFGMI là thiết diện của (P) và chóp