Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D.
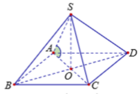
Theo giả thiết S.ABCD là hình chóp tứ giác đều có tất cả các cạnh bằng nhau nên đặt AB = a => SB = a.
Gọi O là tâm của hình vuông ABCD thì 
Xét tam giác SAO vuông tại O có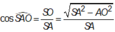 
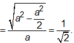
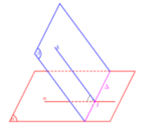
Phương pháp:
Xác định góc giữa hai mặt phẳng 
- Tìm giao tuyến
∆
của 
- Xác định 1 mặt phẳng 
- Tìm các giao tuyến 
- Góc giữa hai mặt phẳng 
Cách giải:
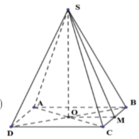
Gọi M là trung điểm của BC. Ta có:
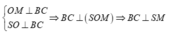
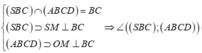
ABCD là hình vuông cạnh a
∆ SOB vuông tại O
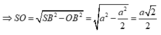
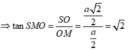
Chọn: A
Chọn B
Thể tích của khối chóp tứ giác đều tất cả các cạnh bằng a là
đáp án D
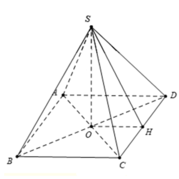
Do S.ABCD là hình chóp tứ giác đều ⇒ S O ⊥ ( A B C D ) .
Gọi K là trung điểm OD
MK sẽ là đường trung bình trong tam giác ∆ S O D
⇒ M K ⊥ ( A B C D )
⇒ tan M B K = M K B K
⇒ tan M B K = M K B K = 1 3
Chọn đáp án D
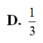
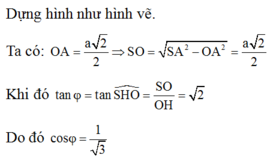
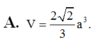
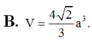
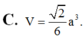
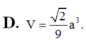
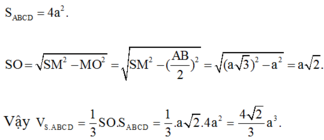
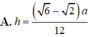
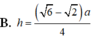
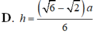
Phương pháp:
+ Sử dụng định nghĩa để tìm góc giữa hai mặt phẳng (P) và (Q):
khi đó góc giữa (P) và (Q) chính là góc giữa hai đường thẳng a và b.
+ Sử dụng định lý hàm số cos trong tam giác để tính toán:
Cho tam giác ABC khi đó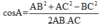
Cách giải:
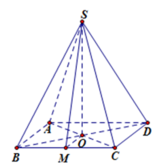
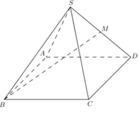
Hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a, ta tìm góc giữa hai mặt phẳng (SAD) và (SBC).
Gọi M, N là trung điểm các cạnh AD và BC, khi đó SM ⊥ AD và SN ⊥ BC (do các tam giác SBC;SAD là các tam giác đều).
Vì BC//AD nên giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng d qua S và song song AD, BC.
Vì SM ⊥ AD và SN ⊥ BC nên SM ⊥ d và SN ⊥ d mà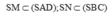
góc giữa hai mặt phẳng (SAD) và (SBC) là góc MSN.
Mặt bên là các tam giác đều cạnh a nên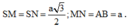
Khi đó: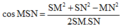
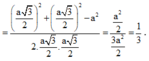
Chọn A
Chú ý khi giải:
Các em có thể tính SO theo tỉ số lượng giác và suy ra MSN = 2MSO