Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
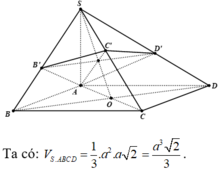
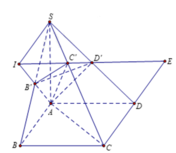
Dựa vào giả thiết ta có B', C', D' lần lượt là hình chiếu của A lên SB, SC, SD.
Tam giác SAC vuông cân tại A nên C' là trung điểm của SC.
Trong tam giác vuông SAB' ta có:
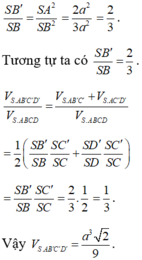


Phương pháp:
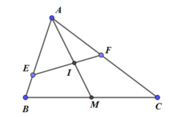
∆ ABC có AM là trung tuyến, I là điểm bất kì trên đoạn AM, đường thẳng đi qua I cắt AB, AC lần lượt tại E, F.
Khi đó: 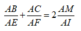
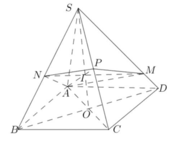
Cách giải:
Ta có: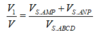
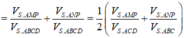

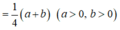
Xét
∆
SAC có: ![]()
![]()
![]()
![]()
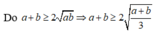
![]()
![]()
Dấu "=" xảy ra 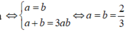
Khi đó 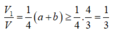
Vậy V 1 V đạt giá trị nhỏ nhất bằng 1 3 khi và chỉ khi a= b = 2 3
Chọn A.

Phương pháp:
Tìm giao điểm C' của SC với (AB'D')
Tính tỉ số S C ' S C
Sử dụng công thức tỉ số thể tích đối với khối chóp tam giác để tính toán.
Cách giải:
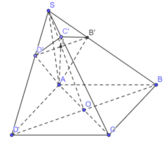
Gọi O là tâm của hình bình hành ABCD. SO cắt B'D' tại I.
Nối AI cắt SC tại C' nên A, B', C', D' đồng phẳng
Đặt ![]()
Ta có: 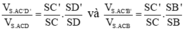
Do đó: 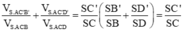
Hay 
![]()
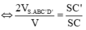
![]()
Xét tam giác ∆ SCO có C', I, A thẳng hàng nên áp dụng định lý Me – ne – la – uýt ta có:
![]()
![]()
Vậy ![]()
![]()
Hay tỷ số thể tích của hai khối đa diện được chia ra bởi (AB'D') là:
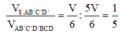
Chọn D.

Đáp án D
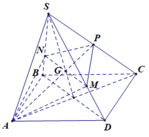
Gọi G là trọng tâm tam giác S A C ⇒ M N đi qua G
Với x = S N S B ; y = S M S D
![]()
![]()
Vậy V 1 V đạt giá trị nhỏ nhất bằng 1 3
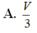
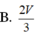
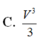
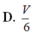
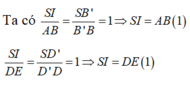
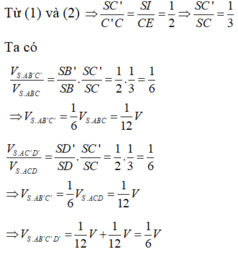
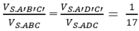
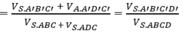
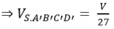

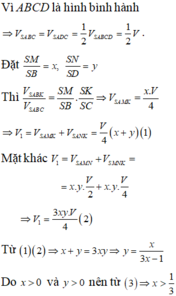
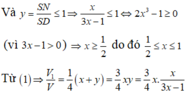


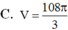
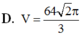

Chọn D
Gọi O là giao điểm của hai đường chéo AC và BD thì SO ∩ DD' = H. Khi đó H là trung điểm của SO và C' = AH ∩ SO.
Trong mặt phẳng (SAC) : Ta kẻ d // AC và AC' cắt (d) tại K. Khi đó áp dụng tính đồng dạng của các tam giác ta có:
Suy ra:
Lưu ý: Có thể sử dụng nhanh công thức: