Mình không thể giải được, có cách giải quyết là cậu chứng minh 2 điểm đó nằm trong 2 tam giác nội tiếp đường tròn thì sẽ thuộc đường tròn

nhưng làm sao để xác định đk 2 điểm đó

Do ABCD là hình thoi \(\Rightarrow\Delta BCD\) cân tại C

Mà \(C=60^0\Rightarrow\Delta BCD\) đều

Hoàn toàn tương tự, ta có tam giác ABD đều

\(\Rightarrow AB=BC=CD=DA=BD\) (1)

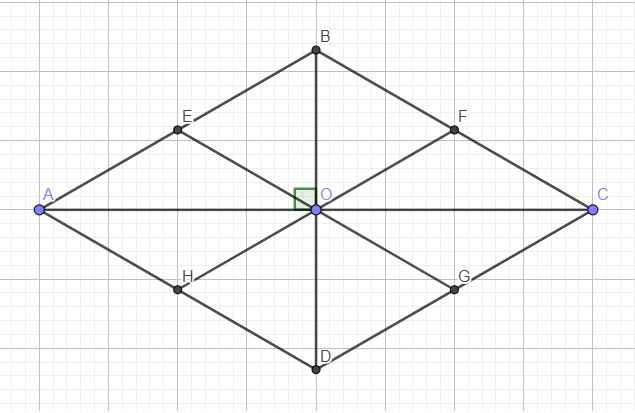
Gọi O là giao điểm 2 đường chéo \(\Rightarrow OA\perp OB\)

Trong tam giác vuông OAB, do E là trung điểm AB nên OE là trung tuyến ứng với cạnh huyền

\(\Rightarrow OE=\dfrac{1}{2}AB\) (2)

Mà O là trung điểm BD (tính chất hình thoi) \(\Rightarrow OB=\dfrac{1}{2}BD\) (3)

(1);(2);(3) \(\Rightarrow OE=OB\)

Hoàn toàn tương tự, ta có: 

\(OE=OB=OF=OG=OD=OH\)

\(\Rightarrow\) Các điểm E, B, F, G, D, H cùng thuộc 1 đường tròn tâm O bán kính OB

a) Chọn điểm O là giao điểm của 2 đường chéo của hình chữ nhật ABCD
⇒ PO là đường trung bình của △ CAM
⇒ PO // AM ⇒ BD//AM
⇒ Tứ giác AMDB là hình thang
b)   Từ a ta có: có AM // BD
⇒     \(\widehat{A_1}=\widehat{B_1}\) ( đồng vị )
Mà △ OAB cân tại O ( vì ABCD là hình chữ nhật )
⇒   \(\widehat{A_2}=\widehat{B_1}\)
⇒  \(\widehat{A_1}=\widehat{A_2}\)    \(\left(1\right)\)
Gọi I là giao điểm của 2 đường chéo của hình chữ nhật AEMF
⇒     △ IEA cân tại I
⇒     \(\widehat{E_1}=\widehat{A_1}\)   \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ⇒  \(\widehat{E_1}=\widehat{A_1}\) ( ở vị trí đồng vị )
⇒ EF // AC  \(\left(3\right)\)
     Mặt khác IP là đường trung bình của △ MAC ( do I,P là trung điểm của AM và BD )
⇒  IP //  AC   \(\left(4\right)\)
Từ \(\left(3\right)\) và \(\left(4\right)\) ⇒ EF  // IP ⇒  Ba điểm E, F, P thẳng hàng
c) Xét△ MAF và △ DBA có:
\(\widehat{MFA}=\widehat{DAB}\)  \(=90^o\)
\(\widehat{A_1}=\widehat{B_1}\) ( cmt ) ;  \(\widehat{A_1}=\widehat{M_1}\)   ( so le trong )
⇒ \(\widehat{B_1}=\widehat{M_1}\)
⇒△ MAF ∼ △ DBA ( g - g )
⇒ \(\dfrac{MF}{DA}=\dfrac{AF}{BA}\)    ⇒    \(\dfrac{MF}{AF}=\dfrac{DA}{BA}\)   ( không đổi )

Xét ΔABD có AB=AD và góc BAD=60 độ

nên ΔABD đều

Ta có: ΔDAB cân tại D

mà DE là đường trung tuyến

nên DE vuông góc với BE

=>E nằm trên đường tròn đường kính BD(1)

Ta có:ΔBAD cân tại B

ma BH là đường trung tuyến

nên BH vuông góc với HD

=>H nằm trên đường tròn đường kính BD(2)

Xét ΔCBD có CB=CD và góc BCD=60 độ

nên ΔCBD đều

Ta có: ΔBDC cân tại D

mà DF là đường trung tuyến

nen DF vuông góc với BF

=>F nằm trên đường tròn đường kính BD(3)

Ta có: ΔBDC cân tại B

mà BG là đường trung tuyến

nên BG vuông góc với GD
=>G nằm trên đường tròn đường kính BD(4)

Từ (1), (2), (3) và (4) suy ra E,B,F,G,D,H cùng nằm trên 1 đường tròn