Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BMDN có
BN//DM
BN=DM
Do đó: BMDN là hình bình hành
Suy ra: BM//DN
b: Ta có: BMDN là hình bình hành
nên BD cắt MN tại trung điểm của mỗi đường(1)
Ta có: ABCD là hình bình hành
nên AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra AC,BD,MN đồng quy

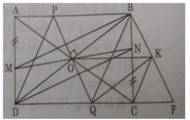
c) PQ ⊥ BD (gt). Xét các tam giác vuông POB và QOD có:
∠POB = ∠QOD∠ (đối đỉnh),
OB = OD
∠PBO = ∠QDO (so le trong).
Do đó ΔPOB = ΔQOD (g.c.g) ⇒ BP = DQ
Lại có BP // DQ nên tứ giác PBQD là hình bình hành
Mặt khác PBQD có hai đường chéo vuông góc nên là hình thoi.

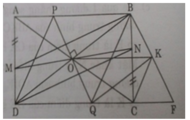
d) Gọi F là giao điểm của BK và QC. Ta có O là trung điểm của BD và OQ // BK (gt) nên Q là trung điểm của DF.
Lại có QK // BD (gt); Q là trung điểm của DF ⇒ K là trung điểm của BF.
CK là trung tuyến của tam giác vuông BCF ⇒ CK = BK = BC/2.
Ta có QK là đường trung bình của tam giác
⇒ QK = BO = BD/2; QK // BO
⇒ Tứ giác OBKQ là hình bình hành
Mặt khác ∠(OBQ) = 90o ⇒ OBKQ là hình chữ nhật
⇒ ∠(OBK) = 90o
Xét ΔOCK và ΔOBK có
CK chung
OC = OB (tính chất đường chéo hình chéo hình chữ nhật)
CK = BK (cmt)
Vậy ΔOCK = ΔOBK (c.c.c) ⇒ ∠OCK = ∠OBK = 90o hay AC ⊥ CK.