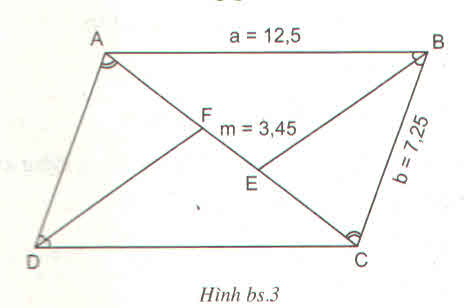
Ta có:

\(\widehat{ABC}=\widehat{ADC}\) và AD = BC = b = 7,25cm vì ABCD là hình bình hành.

Xét hai tam giác ADF và CBE ta có:

\(\widehat{ABC}=\widehat{ADC}\) (cmt)

AD = BC (cmt)

\(\widehat{DAF}=\widehat{BCE}\) (2 góc so le trong)

Vậy \(\Delta ADF=\Delta CBE\) (g-c-g).

=> AF = CE.

Cho AF = CE = x.

Áp dụng tính chất của đường phân giác BE trong tam giác ABC ta có:

\(\dfrac{AB}{BC}=\dfrac{AE}{CE}=\dfrac{AF+FE}{CE}\)

=> \(\dfrac{a}{b}=\dfrac{x+m}{x}=>x=\dfrac{mb}{a-b}\)= \(\dfrac{3,45.7,25}{12,5-7,25}=\dfrac{667}{140}\)

=> AC = \(2x+m=2.\dfrac{667}{140}+3,45=\dfrac{1817}{140}\approx12,98\)

Vậy AC \(\approx12,98\) cm.

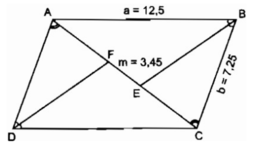
Vì ABCD là hình bình hành nên ∠ ABC =  ∠ ADC.

Mặt khác, BE và DF lần lượt là phân giác của các góc B và D, do đó suy ra  ∠ ADF =  ∠ CBE

Mặt khác, ta có: AD = CB = b;

∠ DAF =  ∠ BCE (so le trong)

Suy ra: △ ADF =  △ CBE (g.c.g)

⇒ AF = CE

Đặt AF = CE = x

Theo tính chất của đường phân giác BE trong tam giác ABC, ta có: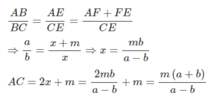

Thay số, tính trên máy tính điện tử cầm tay ta được: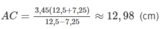

hướng dẫn  thui:

theo tính c hất đường phân giác \(\frac{CN}{AN}=\frac{DC}{AD}=\frac{40.8}{17}\)

\(\frac{AM}{MC}=\frac{AB}{AC}=\frac{40.8}{17}\)\(\Rightarrow\frac{AM}{MC}=\frac{CN}{AN}=\frac{40.8}{17}\)

\(\Rightarrow\frac{AM+MC}{AN+MC}=\frac{40.8}{17}\)\(\Leftrightarrow\frac{2MN+AN+MC}{AN+MC}=\frac{40.8}{17}=\frac{12}{5}\)

\(\frac{2MN}{AC-MN}=\frac{12}{5}-1=\frac{7}{5}\Leftrightarrow\frac{2MN}{\frac{221}{5}-MN}=\frac{7}{5}\)(TÍNH AC DỰA THEO ĐỊNH LÝ PYTAGO)

\(\frac{10}{MN}=839.8-\frac{19}{5}MN\)\(\Rightarrow MN=12.8\left(cm\right)\)

Kẻ đường cao AH.
Ta có: B=2C mà B=HAC (cùng phụ với BAH)
=> HAC=2C
Vì HAC+C=90 độ (tam giác AHC vuông tại H)
2C+C=90 độ
=>3C=90 độ
=>C=30 độ
=> HAC=60 độ
Mà tam giác AHC vuông tại H nên AHC là nửa tam giác đều.
=> AH=AC/2=8/2=4cm
Áp dụng định lý Py-ta-go lần lượt vào 2 tam giác vuông: ABH và AHC
(bn tự tính tìm BH và HC)
Mà BC=BH+HC
(bạn tự tính rồi tìm ra kq)