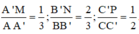Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+ Ta đi xác định đường thẳng ∆:
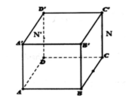
Giả sử đã dựng được đường thẳng ∆ cắt cả AN và A’B. Gọi I; J lần lượt là giao điểm của ∆ với AN và A’B.
Xét phép chiếu song song lên (ABCD) theo phương chiếu A’B.
Khi đó ba điểm J; I; M lần lượt có hình chiếu là B; I’; M
Do J; I; M thẳng hàng nên B; I’; M cũng thẳng hàng. Gọi N’ là hình chiếu của N thì AN’ là hình chiếu của AN.
Vì I thuộc AN nên I’ thuộc AN’
=> I ‘ là giao điểm của BM và AN’.
Từ trên suy ra cách dựng:
+ Gọi I’ là giao điểm của AN’ và BM.
+Trong ( ANN’) dựng II’// NN’( đã có NN’// CD’) cắt AN tại I .
+Vẽ đường thẳng MI, đó chính là đường thẳng cần dựng.
+ Tính tỉ số:
Ta có MC= CN’ suy ra MN’= CD= AB. Do đó I’ là trung điểm của BM.
Mặt khác II’// JB nên II’ là đường trung bình của tam giác MBJ, suy ra IM= IJ nên I M I J = 1
Chọn B

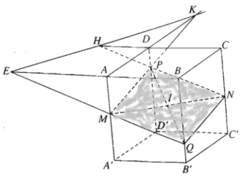
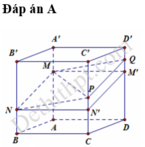
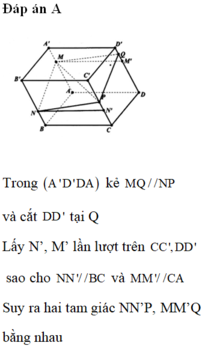
a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB', CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.
Nếu gọi Q là điểm trên cạnh BB' sao cho NQ // PM thì Q là giao điểm của đường thẳng BB' với mặt phẳng (MNP)
Nhận xét. Ta có thể tìm điểm Q bằng cách nối P với trung điểm I của đoạn MN và đường thẳng PI cắt BB' tại Q.
b) Vì mặt phẳng (AA', BB') song song với mặt phẳng (DD', CC') nên ta có MQ // PN. Do đó mặt phẳng (MNP) cắt hình hộp theo thiết diện MNPQ là một ình bình hành.
Giả sử P không phải là trung điểm của đoạn DD'. Gọi H = PN ∩ DC , K = MP ∩ AD. Ta có D = HK là giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
Chú ý rằng giao điểm E = AB ∩ MQ cũng nằm trên giao tuyến d nói trên. Khi P là trung điểm của DD' mặt phẳng (MNP) song song với mặt phẳng (ABCD).

Đáp án C.
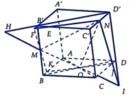
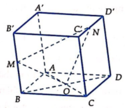
+ Trong mặt phẳng (BB’D’D) gọi I = MO ∩ DD', H = MO ∩ B'D'
Trong mặt phẳng (DD’C’C) gọi J = NI ∩ DC
Trong mặt phẳng (ABCD) gọi K = JO ∩ AB
Trong mặt phẳng (AA’B’B) gọi F = MK ∩ A'B'
Trong mặt phẳng (A’B’C’D’) gọi E = B'C' ∩ FN=> E = BC ∩ (MNO)
![]()
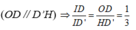
![]()
![]()
![]()

a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB',CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.