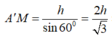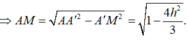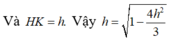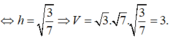Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



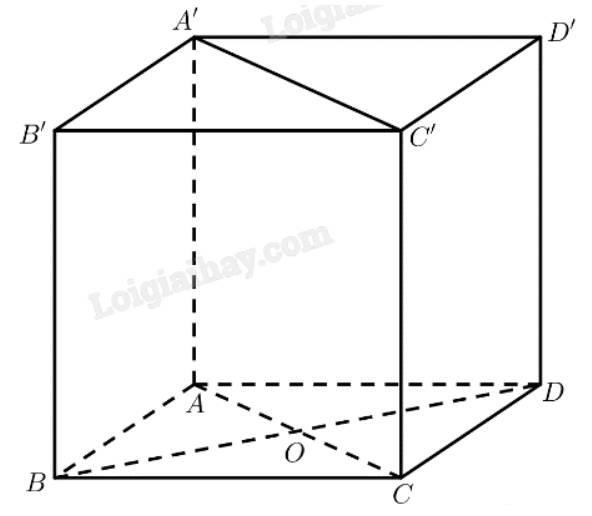
a) Gọi \(O = AC \cap B{\rm{D}}\)
\(ABCD\) là hình thoi \( \Rightarrow AC \bot B{\rm{D}} \Rightarrow AO \bot B{\rm{D}}\)
\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AO\)
\( \Rightarrow d\left( {B{\rm{D}},AA'} \right) = AO = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
b) Tam giác \(OAB\) vuông tại \(O\)
\(\begin{array}{l} \Rightarrow BO = \sqrt {A{B^2} - A{O^2}} = \frac{a}{2} \Rightarrow B{\rm{D}} = 2BO = a\\{S_{ABC{\rm{D}}}} = \frac{1}{2}AC.B{\rm{D}} = \frac{{{a^2}\sqrt 3 }}{2}\\{V_{ABC.A'B'C'}} = {S_{ABC{\rm{D}}}}.AA' = \frac{{3{a^3}}}{4}\end{array}\)

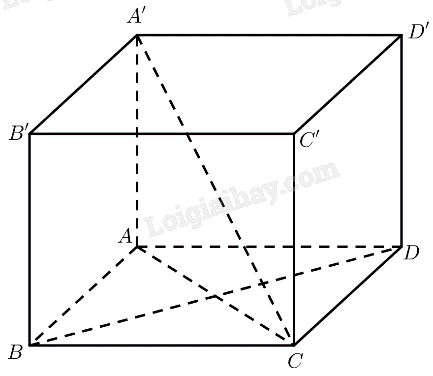
a) Xét tam giác \(AB{\rm{D}}\) có: \(AB = A{\rm{D}} = B{\rm{D}} = a\)
\( \Rightarrow \Delta AB{\rm{D}}\) đều \( \Rightarrow \widehat {BA{\rm{D}}} = {60^ \circ } \Rightarrow \widehat {ABC} = {180^ \circ } - \widehat {BA{\rm{D}}} = {120^ \circ }\)
Xét tam giác \(AB{\rm{C}}\) có:
\(AC = \sqrt {A{B^2} + B{C^2} - 2.AB.BC} = a\sqrt 3 \)
\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AC \Rightarrow \Delta AA'C\) vuông tại \(A\)
\( \Rightarrow AA' = \sqrt {A'{C^2} - A{C^2}} = a\)
b) Ta có:
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = {S_{A'B'C'D'}} = AB.AC.\sin \widehat {BAC} = \frac{{{a^2}\sqrt 3 }}{2}\\{S_{ABB'A'}} = {S_{C{\rm{DD}}'{\rm{C}}'}} = AB.AA' = {a^2}\\{S_{A{\rm{DD}}'A'}} = {S_{BCC'B'}} = A{\rm{D}}.AA' = {a^2}\end{array}\)
Tổng diện tích các mặt của hình hộp là:
\(S = {S_{ABC{\rm{D}}}} + {S_{A'B'C'D'}} + {S_{ABB'A'}} + {S_{C{\rm{DD}}'{\rm{C}}'}} + {S_{A{\rm{DD}}'A'}} + {S_{BCC'B'}} = 2.\frac{{{a^2}\sqrt 3 }}{2} + 4.{a^2} = \left( {4 + \sqrt 3 } \right){a^2}\)

Đáp án A
![]()
![]()
Theo định lí 3 đường vuông góc, ta có
![]()
![]()
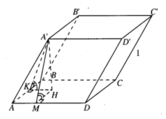
Ta cũng có HKAM là hình chữ nhật, đặt A'H = h ta có