Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

BC=căn 6^2+8^2=10cm
Sxq=(6+8+10)*10=240cm2
Stp=240+2*6*8/2=288cm2
V=1/2*6*8*10=240cm3

Xét tam giác ABC có nửa chu vi của tam giác là:
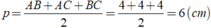
Khi đó ta có
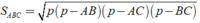

+ Diện tích xung quanh của hình lăng trụ


Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân

a. Thể tích là:
\(\frac{3x4}{2}\)x 9 = 54 cm3
Trong tam giác vuông ABC (vuông tại A), theo định lý Pytago, ta có cạnh huyền bằng:
\(\sqrt{3^2+4^2}\) = 5 cm
Diện tích xung quanh là:
(3 + 4 + 5) x 9 = 108 cm2
Diện tích toàn phần là:
108 + 3 x 4 = 120 cm2
b. Diện tích xung quanh là:
(3 + 4) x 2 x 5 = 70 cm2
Đáp số : 70 cm2

a) Ta có: M là trung điểm của BC(gt)
nên \(BM=CM=\dfrac{BC}{2}=\dfrac{6}{2}=3cm\)
Ta có: ΔABC cân tại A(gt)
mà AM là đường trung tuyến ứng với cạnh đáy BC(M là trung điểm của BC)
nên AM là đường cao ứng với cạnh đáy BC(Định lí tam giác cân)
\(\Rightarrow AM\perp BC\)
Áp dụng định lí Pytago vào ΔABM vuông tại M, ta được:
\(AB^2=AM^2+BM^2\)
\(\Leftrightarrow AM^2=AB^2-BM^2=5^2-3^2=16\)
hay AM=4(cm)
Xét ΔABC có AM là đường cao ứng với cạnh BC(gt)
nên \(S_{ABC}=\dfrac{AM\cdot BC}{2}=\dfrac{4\cdot6}{2}=\dfrac{24}{2}=12cm^2\)
Vậy: Diện tích tam giác ABC là 12cm2
b) Xét tứ giác AMCN có
O là trung điểm của đường chéo AC(gt)
O là trung điểm của đường chéo MN(M và N đối xứng nhau qua O)
Do đó: AMCN là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành AMCN có \(\widehat{AMC}=90^0\)(\(AM\perp BC\))
nên AMCN là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
c) Hình chữ nhật AMCN trở thành hình vuông khi AM=CM
mà \(CM=\dfrac{BC}{2}\)(M là trung điểm của BC)
nên \(AM=\dfrac{BC}{2}\)
Xét ΔABC có
AM là đường trung tuyến ứng với cạnh BC(M là trung điểm của BC)
\(AM=\dfrac{BC}{2}\)(cmt)
Do đó: ΔABC vuông tại A(Định lí 2 về áp dụng hình chữ nhật vào tam giác vuông)
hay \(\widehat{BAC}=90^0\)
Vậy: Khi ΔABC có thêm điều kiện \(\widehat{BAC}=90^0\) thì AMCN là hình vuông

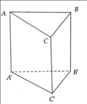
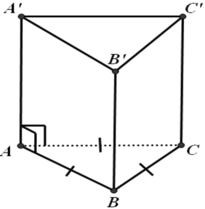
Diện tích xung quanh của lăng trụ là: S x q = P h
Nên chu vi đáy là: P = S x q h = 120 5 = 24 c m
Suy ra chu vi tam giác ABC là 24 cm
Do đó: BC = 24 - AB - AC = 24 - 6 - 8 = 10 cm
Ta thấy 6 2 + 8 2 = 10 2
Theo định lý đảo của định lý Pytago suy ra tam giác ABC là tam giác vuông.
Chọn đáp án D
thank youbanj nha