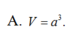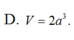Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
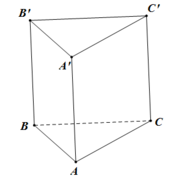
Diện tích đáy là B = S ∆ A B C = a 2 3 4 .
Chiều cao là h = d((ABC); (A'B'C')) = AA'
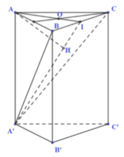
Do tam giác ABC là tam giác đều nên O là trọng tâm của tam giác ABC. Gọi I là trung điểm của BC, H là hình chiếu vuông góc của A lên A'I ta có:
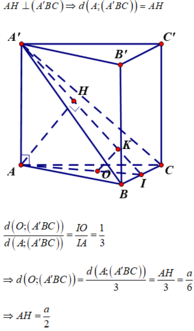
Xét tam giác A'AI vuông tại A ta có:
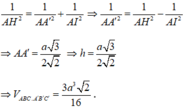

Phương pháp:
Thể tích khối lăng trụ: V = Sh
Cách giải:
Gọi I là trung điểm của BC, kẻ AH ⊥ A'I
∆
ABC đều cạnh a 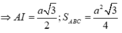
Ta có:
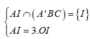
![]()
Ta có: 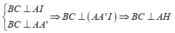
Mà ![]()
![]()
![]()
![]()
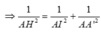
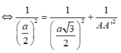
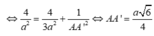
Chọn: A

Chọn D
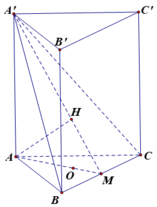
Gọi M là trung điểm của BC và H là hình chiếu của A trên A'M.
Ta có :
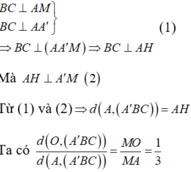
(do tính chất trọng tâm).

Xét tam giác vuông A'AM :
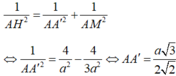
Suy ra thể tích lăng trụ ABC. A'B'C' là:


Từ I dựng IH AC
 IH // AA'
IH // AA'
lại có AA' (ABC) nên HI
(ABC) .
AC//A'B'  CI/AI=AC/A'M=1/2
CI/AI=AC/A'M=1/2
do đó IH/AA'=1/3
V(IABC)=1/3.IH.S(ABC)=1/3.2/3AA'.S(ABC)=2/9V(ABCA'B'C')=2/9.2a.1/2.a.2a=4/9a^3
BC AB và BC
AA'
 BC
BC A'B
A'B==
a
=arctan(A'B/BC)
IC/IA'=2/3 IC=2a
IC=2a
S(IBC)=BC.CI.1/2.sin(arctan(A'B/BC))
Từ đó d(A,IBC)=3.V(IBCA)/S(IBC)
Hạ \(IH\perp AC,\left(H\in AC\right)\Rightarrow IH\perp\left(ABC\right)\)
IH là đường cao của tứ diện IABC
Suy ra IH//AA' \(\Rightarrow\frac{IH}{AA'}=\frac{CI}{CA'}=\frac{2}{3}\)
\(\Rightarrow IH=\frac{2}{3}AA'=\frac{4a}{3}\)
\(AC=\sqrt{A'C-A'A^2}=a\sqrt{5;}BC=\sqrt{AC^2-AB^2}=2a\)
Diện tích tam gia ABC : \(S_{\Delta ABC}=\frac{1}{2}.AB.BC=a^2\)
Vậy thể tích của khối tứ diện IABC : \(V=\frac{1}{3}IH.S_{\Delta ABC}=\frac{4a^3}{9}\)
Hạ \(AK\perp A'B\left(K\in A'B\right)\)
Vì \(BC\perp\left(ABB'A\right)\) nên \(AK\perp BC\) suy ra \(AK\perp\left(IBC\right)\)
Khoảng cách từ A đến mặt phẳng )IBC) là AK
\(AK=\frac{2S_{\Delta AA'B}}{A'B}=\frac{AA'.AB}{\sqrt{AA'^2+AB^2}}=\frac{2a\sqrt{5}}{5}\)

Vì lăng trụ đứng ABC.A'B'C' nên A'A _|_ AC
Xét tam giác A'AC có góc A'AC là góc vuông :
Áp dụng định lý Pytago :
A'C² = A'A² + AC²
<=> AC² = A'C² - A'A²
<=> AC² = (3a)² - (2a)²
<=> AC² = 9a² - 4a²
<=> AC² = 5a²
<=> AC = a√5
Xét tam giác ABC vuông tại B :
Áp dụng định lý Pytago :
AC² = AB² + BC²
<=> BC² = AC² - AB²
<=> BC² = 5a² - a²
<=> BC² = 4a²
<=> BC = 2a
S ABC = (AB.BC)/2 = (a.2a)/2 = a²
Từ I hạ đường IH vuông góc AC , gọi M' là trung điểm của AC ; Gọi I' là giao điểm của M'C' với A'C
Xét tứ giác MC'M'A :
* Có MC' // AM' ( Do A'C' // AC của hình chữ nhật A'C'CA )
* Có MC' = AM' ( Do A'C' = AC của hình chữ nhật A'C'CA )
=> MC'M'A là hình bình hành
=> AM // M'C'
Xét tam giác A'CI'
* M là trung điểm A'C'
* MI // C'I' ( Do AM // M'C' ( cmt ) )
=> I là trung điểm A'I' ( Tính chất đường trung bình )
=> A'I = II' (1)
Xét tam giác A'MI và I'CM'
* Có góc C'A'C = A'CA ( So le trong )
* A'M = M'C
* Có góc A'MA = góc C'M'C ( Do AM // M'C )
=> tam giác A'MI = tam giác I'CM' ( g - c - g )
=> I'C = A'I (2)
Từ (1) ; (2) = > A'I = II' = I'C
=> IC = 2a
Từ đó AH = AC/3 = a√5 / 3
Xét tam giác A'AC và tam giác IHC
* Chung góc C
* Góc A'AC = Góc IHC = 90°
=> Tam giác A'AC ~ Tam giác IHC ( g - g )
=> A'C / IC = AA' / IH
<=> IH = AA'.IC / A'C
<=> IH = 2a.2a / 3a = 4a/3
V IABC = 1/3.S ABC.IH = 1/3.a².4a/3 = 4a^3 / 9
b) Nối HB
Xét tam giác ABC vuông tai B
cosBAC = a/a√5 = 1/√5 = √5/5
Xét tam AHB ;
HB² = AH² + AB² - 2.AH.AB.cosBAC
<=> HB² = (a√5/3)² + a² - 2.(a√5/3).a.√5/5
<=> HB² = 8a²/9
<=> HB = 2a√2 / 3
Xét tam giác IHB vuông tại H
Áp dụng định lý Pytago :
IB² = IH² + HB²
<=> IB² = (4a/3)² + (2a√2/3)²
<=> IB² = 8a/3
<=> IB = 2a√6 / 3
Xét tam giác IBC có IB = 2a√6/3 ; IC = BC = 2a
Áp dụng công thức Hê-rộng :
p = (a + b + c)/2 = (2a√6/3 + 2a + 2a )/2 = a√6/3 + 2a = (6 + √6)a/3
S = √p(p - a)(p - b)(p - c)
S = √[(6 + √6)a(6 - √6)a.√6.a.√6.a ]/81
S = √[6(36 - 6)a^4 / 81]
S = √(180a^4 / 81)
S = √20a^4 / 9
S = 2a²√5 / 3
Từ đó d(A ; IBC ) = V IABC . 3 / S IBC = ( 4a^3 / 9 ).3 / (2a²√5 / 3 ) = 2a√5 / 5

Vì lăng trụ đứng ABC.A'B'C' nên A'A _|_ AC
Xét tam giác A'AC có góc A'AC là góc vuông :
Áp dụng định lý Pytago :
A'C² = A'A² + AC²
<=> AC² = A'C² - A'A²
<=> AC² = (3a)² - (2a)²
<=> AC² = 9a² - 4a²
<=> AC² = 5a²
<=> AC = a√5
Xét tam giác ABC vuông tại B :
Áp dụng định lý Pytago :
AC² = AB² + BC²
<=> BC² = AC² - AB²
<=> BC² = 5a² - a²
<=> BC² = 4a²
<=> BC = 2a
S ABC = (AB.BC)/2 = (a.2a)/2 = a²
Từ I hạ đường IH vuông góc AC , gọi M' là trung điểm của AC ; Gọi I' là giao điểm của M'C' với A'C
Xét tứ giác MC'M'A :
* Có MC' // AM' ( Do A'C' // AC của hình chữ nhật A'C'CA )
* Có MC' = AM' ( Do A'C' = AC của hình chữ nhật A'C'CA )
=> MC'M'A là hình bình hành
=> AM // M'C'
Xét tam giác A'CI'
* M là trung điểm A'C'
* MI // C'I' ( Do AM // M'C' ( cmt ) )
=> I là trung điểm A'I' ( Tính chất đường trung bình )
=> A'I = II' (1)
Xét tam giác A'MI và I'CM'
* Có góc C'A'C = A'CA ( So le trong )
* A'M = M'C
* Có góc A'MA = góc C'M'C ( Do AM // M'C )
=> tam giác A'MI = tam giác I'CM' ( g - c - g )
=> I'C = A'I (2)
Từ (1) ; (2) = > A'I = II' = I'C
=> IC = 2a
Từ đó AH = AC/3 = a√5 / 3
Xét tam giác A'AC và tam giác IHC
* Chung góc C
* Góc A'AC = Góc IHC = 90°
=> Tam giác A'AC ~ Tam giác IHC ( g - g )
=> A'C / IC = AA' / IH
<=> IH = AA'.IC / A'C
<=> IH = 2a.2a / 3a = 4a/3
V IABC = 1/3.S ABC.IH = 1/3.a².4a/3 = 4a^3 / 9
b) Nối HB
Xét tam giác ABC vuông tai B
cosBAC = a/a√5 = 1/√5 = √5/5
Xét tam AHB ;
HB² = AH² + AB² - 2.AH.AB.cosBAC
<=> HB² = (a√5/3)² + a² - 2.(a√5/3).a.√5/5
<=> HB² = 8a²/9
<=> HB = 2a√2 / 3
Xét tam giác IHB vuông tại H
Áp dụng định lý Pytago :
IB² = IH² + HB²
<=> IB² = (4a/3)² + (2a√2/3)²
<=> IB² = 8a/3
<=> IB = 2a√6 / 3
Xét tam giác IBC có IB = 2a√6/3 ; IC = BC = 2a
Áp dụng công thức Hê-rộng :
p = (a + b + c)/2 = (2a√6/3 + 2a + 2a )/2 = a√6/3 + 2a = (6 + √6)a/3
S = √p(p - a)(p - b)(p - c)
S = √[(6 + √6)a(6 - √6)a.√6.a.√6.a ]/81
S = √[6(36 - 6)a^4 / 81]
S = √(180a^4 / 81)
S = √20a^4 / 9
S = 2a²√5 / 3
Từ đó d(A ; IBC ) = V IABC . 3 / S IBC = ( 4a^3 / 9 ).3 / (2a²√5 / 3 ) = 2a√5 / 5