Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tương tự 1A
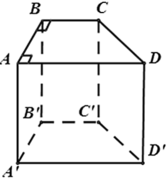
a) AB' và C'D song song, B'D' và AD chéo nhau, AC và A'C' song song.
b) BC' song song với (ADD'A').
c) AC' và CA' cắt nhau tại C.
d) (ACC'A') và (BDD'B') cắt nhau theo giao tuyến OO' (O và O' lần lượt là giao của AC, BD và A'C', B'D')
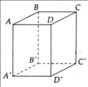

a) Không vì AA' ≠ AB.
b) HS tự chứng minh.
c) Giao tuyến là OO'.
d) Chiều cao là 5 7 c m

Vì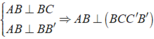
Tương tự: A'B' ⊥ ( BCC'B' ) ⇒ AB,A'B' ⊥ ( BCC'B' )
Chọn đáp án A.

Vì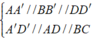
nên các đường thẳng AA',DD',AD,A'D' song song với mặt phẳng ( BCC'B' ).
Chọn đáp án B.

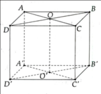
a) Ta có:
- Các đỉnh: A, B, C, A', B' và C'
- Các cạnh bên: AA', BB' và CC'.
- Các cạnh đáy: AB, BC, CA, A'B', B'C' và C'A'.
- Các mặt đáy: ABC và A'B'C'
- Các mặt bên: ABB'A', BCC'B' và CAA'C'
b) AB và CC' chéo nhau, AC và A'B' chéo nhau. Các mặt phẳng (ABB'A') và (BCC'B') cắt nhau theo giao tuyến BB'.
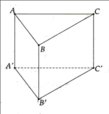

Ta có: A B 2 + A C 2 = B C 2 ⇒ Δ ABC vuông tại A.
Do đó: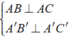
Vì AC vuông góc với hai đường thẳng cắt nhau là AB và AA'
Nên AC ⊥ ( ABB'A' )
Vậy có 3 mặt phẳng vuông góc với ( ABB'A' ) là:
( ABC ), ( A'B'C' ),( ACC'A' )
Chọn đáp án D.

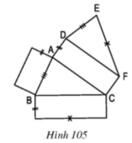
a) Từ hình khai triển bên, ta có thể gấp theo các cạnh để được hình lăng trụ đứng.
b) Các phát biểu đúng:
- Cạnh AD vuông góc với cạnh AB.
- EF và CF là hai cạnh vuông góc với nhau.
- Hai đáy (ABC) và (DEF) nằm trên hai mặt phẳng song song với nhau.

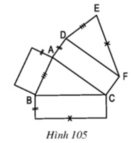
a) Từ hình khai triển bên, ta có thể gấp theo các cạnh để được hình lăng trụ đứng.
b) Các phát biểu đúng:
- Cạnh AD vuông góc với cạnh AB.
- EF và CF là hai cạnh vuông góc với nhau.
- Hai đáy (ABC) và (DEF) nằm trên hai mặt phẳng song song với nhau.

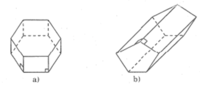
| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Số cạnh của một đáy là: n = d/2 = 20/2 = 10 cạnh
Hình lăng trụ có 20 đỉnh thì :
Số mặt là m = n + 2 = 10 + 2 = 12 mặt
Số cạnh là c = 3n = 3.10 = 30 cạnh
Tương tự 2A
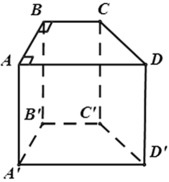
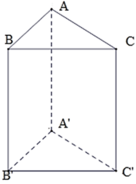
a) (i) Có 8 đỉnh, 12 cạnh và 6 mặt.
(ii) Hình lăng trụ đứng ABDC.A'B'D'C' không là hình hộp chữ nhật vì các đáy không phải là hình chữ nhật.
b) (BCC'B') ^ (ABDC)