Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi mặt phẳng (P) chứa A'C có pt \(ax+by+cz+d=0\)
Do \(A'\left(0;0;1\right);C\left(1;1;0\right)\) \(\Rightarrow\left\{{}\begin{matrix}c+d=0\\a+b+d=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}c=-d\\b=-a-d\end{matrix}\right.\) (1)
\(\left\{{}\begin{matrix}\overrightarrow{n_{\left(P\right)}}=\left(a;b;c\right)\\\overrightarrow{n_{Oxy}}=\left(0;0;1\right)\end{matrix}\right.\) \(\Rightarrow cos\alpha=\frac{\left|c\right|}{\sqrt{a^2+b^2+c^2}}=\frac{1}{\sqrt{6}}\)
\(\Leftrightarrow6c^2=a^2+b^2+c^2\Leftrightarrow5c^2-a^2-b^2=0\) (2)
Thế (1) vào (2):
\(5d^2-a^2-\left(a+d\right)^2=0\Leftrightarrow2d^2-ad-a^2=0\)
\(\Leftrightarrow\left(2d+a\right)\left(d-a\right)=0\Rightarrow\left[{}\begin{matrix}a=d\Rightarrow b=-2d\\a=-2d\Rightarrow b=d\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left(a;b;c\right)=\left(d;-2d;-d\right)=d\left(1;-2;-1\right)\\\left(a;b;c\right)=\left(-2d;d;-d\right)=-d\left(2;-1;1\right)\end{matrix}\right.\)
\(\Rightarrow\)Vecto pháp tuyến của hai mặt phẳng lần lượt là \(\left\{{}\begin{matrix}\overrightarrow{n_1}=\left(1;-2;-1\right)\\\overrightarrow{n_2}=\left(2;-1;1\right)\end{matrix}\right.\)
\(\Rightarrow\) Góc giữa 2 mặt phẳng:
\(cos\beta=\frac{\left|\overrightarrow{n_1}.\overrightarrow{n_2}\right|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}=\frac{\left|2+2-1\right|}{\sqrt{1+4+1}.\sqrt{4+1+1}}=\frac{1}{2}\) \(\Rightarrow\beta=60^0\)

\(AA'=\dfrac{2a}{\sqrt{3}}\)
\(V=AA'\cdot S_{ABCD}=\dfrac{16a^3}{\sqrt{3}}\)

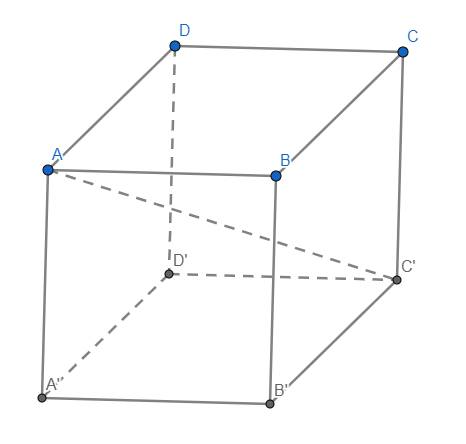
Ta có \(3AB^2=AC'^2=9a^2\) \(\Leftrightarrow AB^2=3a^2\Leftrightarrow AB=a\sqrt{3}\)
\(\Rightarrow V_{hlp}=AB^3=3a^3\sqrt{3}\) (đơn vị thể tích)

\(AC=AB\sqrt{2}=4a\)
Áp dụng định lý Pitago:
\(CC'=\sqrt{\left(AC'\right)^2-AC^2}=3a\)
\(\Rightarrow V=3a.\left(2a\sqrt{2}\right)^2=24a^3\)

Đáp số: \(\dfrac{a\sqrt{2}}{4}\) .
Dễ thấy đường thẳng IJ song song với mặt phẳng (BB'D'D) nên khoảng cách giữa 2 đường thẳng IJ và B'D' bằng khoảng cách giữa đường thẳng IJ và mặt phẳng (BB'D'D) bằng khoảng cách từ điểm J tới mặt phẳng (BB'D'D).
Mặt khác, A'C' vuông góc với B'D' và Đ' nên A'C' vuông góc với (BB'D'D). Gọi O' là giao điểm 2 đường chéo B'D' và A'C'; E là trung điểm đoạn B'O thì JE là đường trung bình tam giác B'OC' nên \(JE\)vuông góc với (BB'D'D) và bằng \(\dfrac{1}{2}OC'=\dfrac{1}{4}A'C'=\dfrac{a\sqrt{2}}{4}\).

Gọi H là hình chiếu vuông góc của A' lên (ABCD)
Do \(A'A=A'B=A'D\) \(\Rightarrow H\) trùng tâm đường tròn ngoại tiếp tam giác ABD
\(\Rightarrow H\) là trung điểm BD
\(AC=\sqrt{AB^2+AD^2}=2a\)\(\Rightarrow AH=\dfrac{1}{2}AC=a\)
\(\Rightarrow A'H=\sqrt{A'A^2-AH^2}=a\sqrt{3}\)
\(\Rightarrow V=A'H.AB.AD=3a^3\)
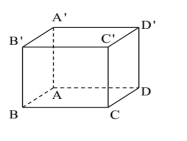 A.3a3 B.a3 C.a3
A.3a3 B.a3 C.a3
Ta có ( CC' , (AB'C)) = ( CC' ,( ADC'B') (1) Có CO vuông góc C'D suy ra CO vg góc ( ADC'B' ) Suy ra (1) = góc CC'O = góc CC'D = 45 độ