Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chứng minh
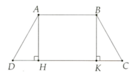
DADH = DBCK (ch-gnh)
Þ DH = CK
Vận dụng nhận xét hình thang ABKH (AB//KH) có AH//BK Þ AB = HK
b) Vậy D H = C D − A B 2
c) DH = 4cm, AH = 3cm; SABCD = 30cm2

Bài 8:
a: Xét ΔDBC có
E là trung điểm của BD
M là trung điểm của BC
Do đó: EM là đường trung bình của ΔDBC
Suy ra: EM//DC
b: Xét ΔAEM có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM
Bài 5:
Xét ΔABC có
\(\dfrac{AE}{EB}=\dfrac{AD}{DC}\left(=1\right)\)
Do đó: DE//BC
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân

Hình ảnh chỉ mang tính chất minh họa
Ta có: AB=HK=3cm
=> DH=KC=(DC-HK):2=1,5cm
=> DK=DH+HK=4,5 cm
Theo định lí pitago trong tam giác vuông AHD có:
\(AH=\sqrt{AD^2-DH^2}=\sqrt{2,5^2-1,5^2}=2cm\)
Tương tự:
\(AK=\sqrt{AH^2+HK^2}=\sqrt{2^2+3^2}=\sqrt{13}cm\)

Lời giải:
Xét tam giác $ADH$ và $BCK$ có:
$\widehat{AHD}=\widehat{BKC}=90^0$
$\widehat{ADH}=\widehat{BCK}$ (do $ABCD$ là htc)
$AD=BC$ (do $ABCD$ là htc)
$\Rightarrow \triangle ADH=\triangle BCK$ (ch-gn)
$\Rightarrow DH=CK$
Áp dụng định lý Pitago cho tam giác $ADH$ vuông:
$AH=\sqrt{AD^2-DH^2}=\sqrt{10^2-6^2}=8$ (cm)
Từ tam giác bằng nhau ở trên suy ra $BK=AH=8$ (cm)

a: Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
\(\widehat{D}=\widehat{C}\)
Do đó: ΔAHD=ΔBKC
=>DH=CK
b: DH=CK
mà DH=9
nên CK=9
ΔAHD vuông tại H
=>\(AH^2+HD^2=AD^2\)
=>\(AH^2=15^2-9^2=144\)
=>AH=12
Xét tứ giác ABKH có
AH//BK
AH=BK
Do đó: ABKH là hình bình hành
mà \(\widehat{AHK}=90^0\) và AB=AH
nên ABKH là hình vuông
=>AB=AH=HK=12
DC=DH+HK+KC
=12+9+9
=30