Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Xét △DMI có: AB//DM.
\(\Rightarrow\dfrac{AB}{DM}=\dfrac{IA}{IM}\) (hệ quả định lí Ta-let)
a. Xét △CMK có: AB//CM.
\(\Rightarrow\dfrac{AB}{CM}=\dfrac{KB}{KM}\) (hệ quả định lí Ta-let)
Mà \(DM=CM\) (M là trung điểm DC)
\(\Rightarrow\dfrac{AB}{DM}=\dfrac{KB}{KM}\)
-Xét △ABM có: \(\dfrac{IA}{IM}=\dfrac{KB}{KM}\left(=\dfrac{AB}{DM}\right)\)
\(\Rightarrow\)IK//AB (định lí Ta-let đảo).
b) -Xét △ADM có: EI//DM.
\(\Rightarrow\dfrac{EI}{DM}=\dfrac{AI}{AM}\) (hệ quả định lí Ta-let)
-Xét △ACM có: KI//CM.
\(\Rightarrow\dfrac{IK}{CM}=\dfrac{AI}{AM}\) (hệ quả định lí Ta-let)
Mà \(DM=CM\) (M là trung điểm DC)
\(\Rightarrow\dfrac{IK}{DM}=\dfrac{AI}{AM}=\dfrac{EI}{DM}\) nên \(IK=EI\).
-Xét △BCM có: KF//CM.
\(\Rightarrow\dfrac{KF}{CM}=\dfrac{BK}{BM}\) (hệ quả định lí Ta-let)
-Xét △BDM có: IK//DM.
\(\Rightarrow\dfrac{IK}{DM}=\dfrac{BK}{BM}\) (hệ quả định lí Ta-let)
Mà \(DM=CM\) (M là trung điểm DC)
\(\Rightarrow\dfrac{IK}{CM}=\dfrac{BK}{BM}=\dfrac{KF}{CM}\) nên \(IK=KF\)
-Vậy \(EI=IK=KF\)

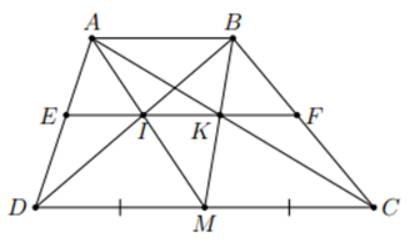
a) Vì AB // CD áp dụng định lý Ta-lét ta có:
\(\dfrac{IM}{IA}\)=\(\dfrac{MD}{AB}\)
\(\Rightarrow\) \(\dfrac{IM}{IA}\)=\(\dfrac{KM}{KB}\) (Vì MC = MD)
\(\dfrac{KM}{KB}\)=\(\dfrac{MC}{AB}\)
Do đó theo định lý Ta-lét đảo ta có IK // AB
Vì IK // AB // CD nên theo định lý Ta-lét :
\(\dfrac{IE}{DM}\)=\(\dfrac{AI}{AM}\)=\(\dfrac{BI}{BD}\)=\(\dfrac{IK}{DM}\)=> EI = IK
Tương tự ta có FK =IK nên ta có EI = IK = KF

a: Xét ΔIAB và ΔIMD có
góc IAB=góc IMD
góc AIB=góc MID
=>ΔIAB đồng dạng với ΔIMD
=>IA/IM=AB/MD=IB/ID
Xét ΔKAB và ΔKCM có
góc KAB=góc KCM
góc AKB=góc CKM
=>ΔKAB đồng dạng với ΔKCM
=>KA/KC=KB/KM=AB/CM
KB/KM=AB/CM
AI/IM=AB/MD
mà CM=MD
nên KB/KM=AI/IM
=>MI/IA=MK/KB
Xét ΔMAB có MI/IA=MK/KB
nên IK//AB
b: Xét ΔAMC có IK//MC
nên IK/MC=AI/AM
Xét ΔADM có EI//DM
nên EI/DM=AI/AM
Xét ΔBMC có KF//MC
nên KF/MC=BK/BM
Xét ΔMAB có IK//AB
nên AI/AM=BK/BM
=>IK/MC=FK/MC=EI/DM
mà MC=DM
nên IK=FK=EI

a: Xét ΔKAB và ΔKCM có
góc KAB=góc KCM
góc AKB=góc CKM
=>ΔKAB đồng dạng với ΔKCM
=>KB/KM=AB/CM=AB/MD
Xét ΔIAB và ΔIMD có
góc IAB=góc IMD
góc AIB=góc MID
=>ΔIAB đồng dạng với ΔIMD
=>IA/IM=AB/MD
=>IA/IM=KB/KM
=>MI/IA=MK/KB
Xét ΔMAB có MI/IA=MK/KB
nên IK//AB
b: Xét ΔADM có EI//DM
nên EI/DM=AI/AM
=>EI/CM=AI/AM
Xét ΔBMC có KF//MC
nên KF/MC=BK/BM
Xét ΔMAB có IK//AB
nên IK/AB=MK/MB=MI/MA
=>BK/BM=AI/AM
=>EI/DM=KF/DM
=>EI=KF
c: Xét ΔOAN và ΔOCM có
góc OAN=góc OCM
góc AON=góc COM
=>ΔOAN đồng dạng với ΔOCM
=>OA/OC=AN/CM
Xét ΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOb=góc COD
=>ΔOAB đồng dạng với ΔOCD
=>OA/OC=AB/CD
=>AB/CD=AN/CM
=>AB/AN=CD/CM=2
=>AB=2AN
=>N là trung điểm của AB

Ta có: AB//CD => AB//DM
=> \(\frac{AI}{IM}=\frac{AB}{DM}\)
AB// MC
=> \(\frac{BK}{KM}=\frac{AB}{MC}\)
Mà DM=MC
=> \(\frac{AI}{IM}=\frac{BK}{KM}\)=> IK//AB
b) IK//AB
=> EI//DM => \(\frac{EI}{DM}=\frac{AI}{AM}\)
IK//MC => \(\frac{AI}{AM}=\frac{IK}{MC}=\frac{BK}{BM}\)
KF//MC => \(\frac{BK}{BM}=\frac{KF}{MC}\)
=> \(\frac{EI}{DM}=\frac{IK}{MC}=\frac{KF}{MC}\)Mà DM =MC
=> EI=IK=KF

hình thang ABCD (AB // CD) , E và F lần lượt là trung điểm của AD và BC
=>EF là đường trung bình của hình thang ABCD
=> EF // AB (1)
EF // CD (2)
tam giác ABC có F là trung điểm của BC
từ (1) => FK là đường trung bình của tam giác ABC
=> K là trung điểm của AC
=> AK = KC
tam giác ADC có E là trung điểm của AD
từ (2) => FK là đường trung bình của tam giác ADC
=> I là trung điểm của BD
=> BI = ID
sửa giùm
tam giác ABD có E là trung điểm của AD
từ (2) => EI là đường trung bình của tam giác ABD
=> I là trung điểm của BD
=> BI = ID