Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

Gọi H là trung điểm DC.
Chứng minh HE// IF( vì cùng //BC)
=> HE vuông FK ( vì FK vuông IF)
Tương tự HF// EI( vì cùng //AD)
=> HF vuông EK( vì EK vuông IE)
Xét tam giác EFH có EK và FK là 2 đường cao nên K là trực tâm. Suy ra HK vuông FE mà FE //DC nên HK vuông DC tại H suy ra tam giác KDC cân tại K. Nên KD=KC

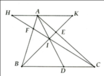
a: Xét ΔODK có AH//DK
nên AH/DK=OH/OK
Xét ΔOKC có HB//KC
nên HB/KC=OH/OK
=>AH/DK=HB/KC
mà AH=HB
nên DK=KC
=>K là trung điểm của CD
b: Xét ΔMAB và ΔMKD có
góc MAB=góc MKD
góc AMB=góc KMD
Do đo: ΔMAB đồng dạng với ΔMKD
=>MA/MK=AB/DK
=>MK/MA=DK/AB
Xét ΔNKC và ΔNBA có
góc NKC=góc NBA
góc KNC=góc BNA
Do đó: ΔNKC đồng dạng với ΔNBA
=>NK/NB=KC/BA=KD/AB=MK/MA
=>MN//AB