Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

kẻ BK\(\perp\)DC
Xét ΔAHD vuông tại H có \(tanD=\dfrac{AH}{HD}\)
=>\(\dfrac{5}{HD}=tan45=1\)
=>HD=5/1=5(cm)
Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
\(\widehat{D}=\widehat{C}\)
Do đó: ΔAHD=ΔBKC
=>DH=KC
mà DH=5cm
nên KC=5cm
Ta có: AB//DC
\(H,K\in DC\)
Do đó: AB//HK
Ta có: AH\(\perp\)DC
BK\(\perp\)DC
Do đó: AH//BK
Xét tứ giác ABKH có
AB//KH
AH//BK
Do đó: ABKH là hình bình hành
=>AB=HK=3cm
DC=DH+HK+KC
=5+5+3
=13(cm)

Đáp án cần chọn là: B
Ta có tam giác ADH vuông cân tại H vì D ^ = 450.
Do đó DH = AH = 6cm
Mà DH = 1 2 (CD – AB)
Suy ra CD = 2DH + AB = 12 + 4 = 16 (cm)
Vậy CD = 16 cm.

Đáp án cần chọn là: C

Ta có DH = 1 2 (CD – AB) = 1 2 (22 – 12)
Do ABCD là hình thang cân nên AD = BC = 13 cm
Áp dụng định lí Py-ta-go vào tam giác ADH vuông tại H ta có
A D 2 = A H 2 + D H 2 ⇒ A H 2 = A D 2 - D H 2 = 13 2 - 5 2 ⇒ A H = 12
Vậy AH = 12cm.

Do AB//CD
=) \(\widehat{A}\)+\(\widehat{D}\)=1800 (2 góc vị trí trong cùng phía )
1000 + \(\widehat{D}\)=1800
\(\widehat{D}\)=1800 - 1000
\(\widehat{D}\)= 800
Xét tứ giác ABCD có :
\(\widehat{A}\)+\(\widehat{B}\)+\(\widehat{C}\)+\(\widehat{D}\)=3600
1000+1200+\(\widehat{C}\)+800 =3600
3000 +\(\widehat{C}\)=3600
\(\widehat{C}\)= 600
2) Từ B kẻ BE \(\perp\)CD
Xét tam giác ADH (\(\widehat{AH\text{D}}\)=900) và BCE (\(\widehat{BEC}\)=900) có:
AD=BC (tính chất hình thang cân)
\(\widehat{A\text{D}H}\)=\(\widehat{BCE}\)(tính chất hình thang cân)
=) Tam giác ADH = Tam giác BCE (cạch huyền - góc nhọn )
=) DH= CE (2 cạch tương ứng )
Do AB//CD Mà AH\(\perp\)CD=) AH\(\perp\)AB
Xét tứ giác ABEH có
\(\widehat{BAH}\)= \(\widehat{AHE}\) = \(\widehat{BEH}\) = 900
=) Tứ giác ABEH lá hình chữ nhật =) AB=HE=10 cm
Ta có : DH+HE+EC= 20 cm
2DH+10=20
2DH =10
DH = 5 (cm)
xét tam giác vuông AHD
Áp dụng định lí Pitago ta có
AD2=AH2+HD2
AD2=122+52
AD2= 144+25=169
AD=13 cm (đpcm)

a: Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
Do đó: ΔADC=ΔBCD
Suy ra: \(\widehat{CAD}=\widehat{DBC}\)
b: Ta có: ΔADC=ΔBCD
nên \(\widehat{ODC}=\widehat{OCD}\)
hay ΔOCD cân tại O
Suy ra: OC=OD
hay OA=OB

Đáp án cần chọn là: B

Kẻ BK ⊥ DC tại K.
Vì ABCD là hình thang cân nên ta có D ^ = C ^ ; AD = BC
=> ΔAHD = ΔBKC (ch – gn) => DH = CK
Suy ra DH = 1 2 (CD – AB)
Suy ra DH = 1 2 (CD – AB) = 1 2 (10 – 4)
Do ABCD là hình thang cân nên AD = BC = 5 cm
Áp dụng định lí Py-ta-go vào tam giác ADH vuông tại H ta có
A D 2 = A H 2 + D H 2 ⇒ A H 2 = A D 2 - D H 2 = 5 2 - 3 2 ⇒ A H = 4
Vậy AH = 4cm.

Bài 2:
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{ACB}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)
Đáp án cần chọn là: A.
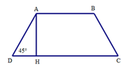
Ta có tam giác ADH vuông cân tại H vì D ^ = 45 ° .
Do đó DH = AH = 5cm
Mà DH = 1 2 (CD – AB)
Suy ra CD = 2DH + AB = 2.5 + 3 = 13 (cm)
Vậy CD = 13 cm