Chiều cao của hình HCN đó là:

`(6x^2y - 8xy^2) \div 2xy`

`= 6x^2y \div 2xy - 8xy^2 \div 2xy`

`= 3x - 4y`

Chiều cao là: `V : S = (6x^2y - 8xy^2) : 2xy = 3x - 4y`.

\(S=\dfrac{1}{2}\cdot6y\cdot\left(x+2+x+3\right)=\dfrac{1}{2}\cdot6y\cdot\left(2x+5\right)\)

\(S=\dfrac{1}{2}\cdot6y\left(2x+5\right)=3y\left(2x+5\right)\)

Chọn C

cảm ơn

gọi độ dài của đáy lớn là: x (đơn vị: cm, x>4)

`->` độ dài của đáy nhỏ là: `x-4` `(cm)`

độ dài của chiều cao là: `1/2x` `(cm)`

diện tích hình thang là

`(x+x-4)xx1/2x:2`

`=(2x-4)xx1/4x`

`=1/2x^2 -x`

a) x⁴+x³+2x²+x+1=(x⁴+x³+x²)+(x²+x+1)=x²(x²+x+1)+(x²+x+1)=(x²+x+1)(x²+1)

b)a³+b³+c³-3abc=a³+3ab(a+b)+b³+c³ -(3ab(a+b)+3abc)=(a+b)³+c³-3ab(a+b+c)

=(a+b+c)((a+b)²-(a+b)c+c²)-3ab(a+b+c)=(a+b+c)(a²+2ab+b²-ac-ab+c²-3ab)=(a+b+c)(a²+b²+c²-ab-ac-bc)

c)Đặt x-y=a;y-z=b;z-x=c

a+b+c=x-y-z+z-x=o

đưa về như bài b

d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung

e)x²(y-z)+y²(z-x)+z²(x-y)=x²(y-z)-y²((y-z)+(x-y))+z²(x-y)

=x²(y-z)-y²(y-z)-y²(x-y)+z²(x-y)=(y-z)(x²-y²)-(x-y)(y²-z²)=(y-z)(x²-2y²+xy+xz+yz)

Câu 1

X^3+Y3+z^3-3xyz = (x+y+z)(x^2+y^2+z^2 -xy-yz-zx) =0. Nên chỉ có 2 TH

a) TH1: x+y+z = 0 --> x+y=-z; y+z=-x; z+x=-y (1):

Biến đổi P= (x+y)(y+z)(z+x)/xyz (2). Thay (1) vào (2) được P = -xyz/xyz = -1

b) TH2: x^2+y^2+z^2 -xy-yz-zx --> x=y=z. Thay vào biểu thức của P được P = (1+1)(1+1)(1+1)=8

Câu 3 

x^2+y^2 >= 2xy

y^2+z^2 >= 2yz

z^2+x^2>=2xz

Cộng 2 vế với vế cuae 3 BDT trên được 2(x^2+y^2+x^2)>=2(xy+yz+zx) --> x^2+y^2+x^2>= xy+yz+zx (1) Dấu = xảy ra khi x=y=z

Mặt khác A=(x+y+z)^2=x^2+y^2+x^2+2(xy+yz+zx)=9. Theo (1) A>=xy+yz+zx+2(xy+yz+zx) = 3(xy+yz+zx)

nên 9>=3(xy+yz+zx) --> 3>=xy+yz+zx. Vậy giá trị lớn nhất của P là 9. Khi đó x=y=z=1

– Biểu thức tính diện tích mảnh vườn trên theo x và y là:

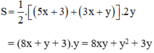
– Nếu x = 3 mét và y = 2 mét thì diện tích mảnh vườn là:

S = 8.3.2 + 22 + 3.2 = 58 (m2).