Xét tam giác ABD và BDC có:

B A D ^ = D B C ^ = 60 ∘

A B D ^ = B D C ^ (so le trong)

⇒ Δ A B D   đ ồ n g   d ạ n g   Δ B D C   g ,   g ⇒ A B B D = B D D C ⇒ B D 2 = A B . D C = 4.9 = 36 ⇒ B D = 6 c m

Đáp án: D

3)áp dụng pytago để tính

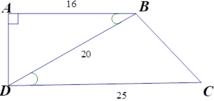
ΔABD và ΔBDC có góc ABD = BDC (hai góc ở vị trí so le trong bằng nhau do AB // CD);

Và A B B D = B D D C (vì 16 20 = 20 25 )

Do đó ΔABD ~ ΔBDC (c.g.c)

Đáp án: A

a) CE = BC – BE = 25 – 9 =16 = CD

Tam giác ABE cân tại B => góc BAE = góc BEA

Tam giác CED cân tại C => góc CED = góc CDE

=> góc BEA + góc CED

= góc BAE + góc CDE

= 90 độ - góc EAD + 90 độ - góc ADE

= 180 độ - (góc EAD + góc ADE)

=180 độ - (180 độ - góc AED)

=góc AED

=> góc BEA + góc CED=góc AED

Mà góc BEA + góc CED + góc AED = 180 độ

=> góc BEA + góc CED=góc AED = 90 độ

Mày nhìn cái chóa j

Sử dụng định lý pi - ta - go nha

Biết tính cạnh AD thôi ^^!

Áp dụng định lý Py-ta-go vào tam giác vuông ADC:

AD^2 + DC^2 = AC^2 

=> AD^2 = AC^2 - DC^2 = 17^2 - 15^2 = 289 - 225 = 64 

\(\Rightarrow AD=\sqrt{64}=8\left(cm\right)\)