Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

 giải
giải
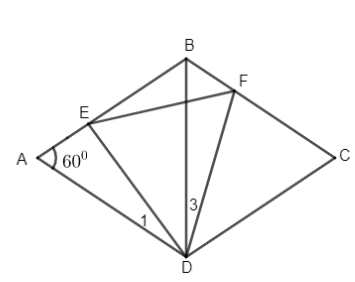
ta có AB=AD(gt)và góc A=60 độ nên tam giác DEF đều=>BD=AD
Tương tự tam giác DEF đều =>góc CBD=60độ
Từ BE+BF=BD=>AE=BF
Xét tam giác AED và tam giác BFD có:
AD=BD(cmt)
góc A=góc CBD=60 độ
AE=BF
Do đó tam giác AED=tam giác BFD(c,g.c)
=>DE=DF
nên tam giác DEF cân (1)
Và góc D1=góc D3 nên góc D1+góc EBD=60độ =>góc D3+góc EBD=60độ (2)
Từ (1) và (2) suy ra tam giác DEF đều.

Sửa đề: BC=2AB
a: \(BE=EC=\dfrac{BC}{2}\)
\(AF=FD=\dfrac{AD}{2}\)
mà BC=AD
nên BE=EC=AF=FD
Xét tứ giác ABEF có
BE//AF
BE=AF
Do đó: ABEF là hình bình hành
mà BE=BA(=1/2BC)
nên ABEF là hình thoi
b: Xét ΔIFA có
FB là đường trung tuyến
\(FB=\dfrac{IA}{2}\)
Do đó: ΔIFA vuông tại F
=>IF\(\perp\) AD
mà AD//BC
nên \(IF\perp BC\)
c: Xét tứ giác BICD có
BI//CD
BI=CD
Do đó: BICD là hình bình hành
=>BC cắt ID tại trung điểm của mỗi đường
mà E là trung điểm của BC
nên E là trung điểm của ID
=>I,E,D thẳng hàng
Ta có ABCD là hình thoi nên \(AD=AB\)
Mà \(\widehat{A}=60^0\) nên ABD đều
Lại có BD là phân giác \(\widehat{ABC}\Rightarrow\widehat{ABD}=\widehat{DBC}=60^0\)
\(\left\{{}\begin{matrix}BE+BF=BD=AB\\AE+BE=AB\end{matrix}\right.\Rightarrow AE=BF\)
\(\left\{{}\begin{matrix}AE=BF\\AD=BD\\\widehat{DAE}=\widehat{DBF}=60^0\end{matrix}\right.\Rightarrow\Delta DEA=\Delta DFB\left(c.g.c\right)\\ \Rightarrow DE=DF\)
Do đó DEF cân tại D
Mà \(\widehat{ADE}=\widehat{BDF}\left(\Delta DEA=\Delta DFB\right)\)
\(\Rightarrow\widehat{ADE}+\widehat{EDB}=\widehat{BDF}+\widehat{EDB}\\ \Rightarrow\widehat{ADB}=\widehat{EDF}=60^0\)
Vậy tam giác DEF đều