Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

http://lazi.vn/edu/exercise/cho-tu-giac-abcd-goi-m-n-p-q-lan-luot-la-trung-diem-cua-cac-canh-ab-cd-ad-bc-chung-minh-vecto-mp-qn-mq-pn . Bạn vào link này nhé


a) Ta có AB = CD (cạnh hình thoi)
BE = DG (gt)
⇒ AB + BE = CD + DG hay AE = CG (cmt)
Xét ΔAHE và ΔCFG có:
AE = CG
∠HAE = ∠FCG (cùng bù với ∠BAD = ∠DCB ),
AH = CF (gt)
Do đó ΔAHE = ΔCFG (c.g.c) ⇒ HE = FG
Chứng minh tương tự ta có HG = EF
Do đó tứ giác EFGH là hình bình hành (các cạnh đối bằng nhau).
b) Nối E và G.
Xét ΔOBE và ΔODG có
BE = DG (gt),
∠OBE = ∠ODG (so le trong),
OB = OD ( tính chất đường chéo của hình thoi ABCD)
⇒ ΔOBE = ΔODG (c.g.c) ⇒ ∠OBE = ∠ODG
Mà ∠DOG + ∠GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.
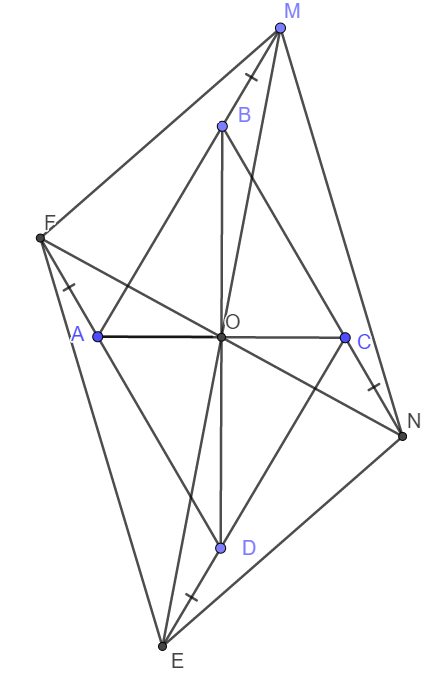
c) Hình bình hành EFGH là hình thoi ⇔ HE = EF
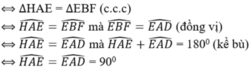
⇔ Hình thoi ABCD có 1 góc vuông
⇔ ABCD là hình vuông.
Vậy hình thoi ABCD phải là hình vuông thì hình bình hành EFGH trở thành hình thoi.

a) Do ABCD là hình thoi nên \(\widehat{BAD}=\widehat{DCB}\)
Suy ra \(\widehat{FAM}=\widehat{NCE}\)
Cũng do ABCD là hình thoi nên AB = CD, hay AM = CE
Xét tam giác FAM và tam giác NCE có:
FA = NC
AM = CE
\(\widehat{FAM}=\widehat{NCE}\)
\(\Rightarrow\Delta FAM=\Delta NCE\left(c-g-c\right)\)
b) Từ câu a ta có: FM = NE
Chứng minh tương tự câu a thì \(\Delta EDF=\Delta MBN\left(c-g-c\right)\Rightarrow FE=NM\)
Xét tứ giác MNEF có FM = NE, FE = MN nên MNEF là hình bình hành.
c) Gọi O là giao điểm của AC và BD. Do ABCD là hình thoi nên O là trung điểm AC và BD.
Xét tứ giác AFCN có FA song song và bằng CN nên AFCN là hình bình hành.
Suy ra FN cắt AC tại trung điểm mỗi đường. Suy ra O là trung điểm FN.
Tương tự BMDE là hình bình hành nên O là trung điểm ME.
Tóm lại O là trung điểm của FN và ME hay O là giao điểm hai đường chéo của cả hình bình hành MNEF và hình thoi ABCD.
bài c mk có cách giải kc rùi nhưng cx cảm ơn bk và mk k cho bạn