


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




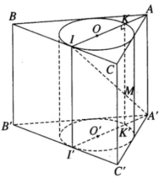
Hình trụ nội tiếp trong lăng trụ tam giác đều có đường tròn đáy tiếp xúc tại trung điểm các cạnh của tam giác đáy. Gọi I là trung điểm của cạnh BC, r là bán kính đáy của hình trụ nội tiếp trong lăng trụ
Ta có: 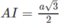
Do đó: 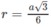
Ta có diện tích xung quanh của hình trụ nội tiếp lăng trụ là:
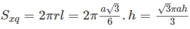

Đáp án B
Từ giả thiết ta có đường cao của hình trụ là độ dài cạnh bên của lăng trụ và bán kính đường tròn đáy là bán kính đường tròn ngoại tiếp tam giác ABC nên ta có 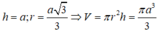

Đáp án B
Gọi ABCD.A'B'C'D' là hình lăng trụ nội tiếp hình trụ. Khi đó lăng trụ đã cho là lăng trụ đứng và có chiều cao là chiều cao h của hình trụ. Vậy thể tích khối lăng trụ đạt giá trị lớn nhất khi và chỉ khi diện tích đáy ABCD đạt giá trị lớn nhất. Do ABCD nội tiếp đường tròn đáy của hình trụ nên ta có:
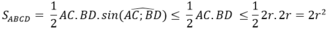
Dấu bằng xảy ra khi ABCD là hình vuông. Vậy thể tích khối lăng trụ tứ giác nội tiếp hình trụ lớn nhất là V = 2 r 2 h

Chọn A
Xét hình lăng trụ đều (H) đã cho có đáy là đa giác đều n đỉnh. Xét điểm trong I của hình lăng trụ đều (H) đã cho. Khi đó nối I với các đỉnh của (H) ta được n+2 khối chóp có đỉnh là I, trong đó có hai khối chóp có đỉnh là I và mặt đáy là mặt đáy của (H); và n khối chóp có đỉnh I và mặt đáy là mặt bên của (H). Diện tích mỗi mặt
đáy của (H) bằng S; diện tích mỗi mặt bên của (H) bằng ah. Gọi h1, h2, .., hn, hn+1, hn2 lần lượt là khoảng cách từ I đến các mặt bên của (H) và các mặt đáy của (H). Vậy theo công thức tính thể tích của khối lăng trụ và khối chóp ta có:
![]()
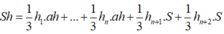
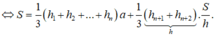
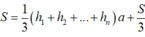
![]()
Chú ý tổng khoảng cách từ I đến hai mặt đáy của (H) là ![]()


Ta có : \(\dfrac{KM}{AA'}=\dfrac{IK}{IA}=\dfrac{2}{3}\Rightarrow KM=\dfrac{2}{3}h\)
Xét tam giác vuông IKM ta có : \(IM^2=IK^2+KM^2=\dfrac{3a^2}{9}+\dfrac{4h^2}{9}=\dfrac{3a^2+4h^2}{9}\)
Vậy :
\(IM=\dfrac{\sqrt{3a^2+4h^2}}{3}\)