Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

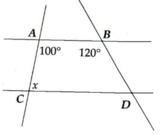
Vì \(AB//CD\) nên \(\widehat{BAC}+\widehat{CAD}=180^0\)(2 góc trong cùng phía)
\(\Rightarrow\widehat{CAD}=180^0-\widehat{BAC}=180^0-100^0=80^0\\ \Rightarrow x=80^0\)
Ta có: a//b(gt)
\(\Rightarrow\widehat{BAC}+\widehat{ACD}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{ACD}=180^0-\widehat{BAC}\)
\(\Rightarrow x=180^0-100^0=80^0\)

\(a//b\) nên \(\widehat{CAB}+\widehat{ACD}=180^0\left(2.góc.trong.cùng.phía\right)\)
Hay \(x+100^0=180^0\Rightarrow x=80^0\)

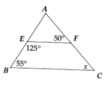
Ta có \(\widehat{FEB}+\widehat{EBC}=125^0+55^0=180^0\)
Mà 2 góc này ở vị trí trong cùng phía nên \(EF//BC\)
Do đó \(\widehat{AFE}=\widehat{ACB}=50^0\)(2 góc đồng vị)
\(\Rightarrow x=\widehat{ACB}=50^0\)


Xét tam giác ABC có:
\(\widehat{BEF}+\widehat{EBC}=125^0+55^0=180^0\)
Mà 2 góc này là 2 góc kề bù
=> EF//BC
=> \(\widehat{AFE}=\widehat{ACB}\)(2 góc đồng vị)
\(\Rightarrow x=50^0\)

Bạn tham khảo link này nha ! Có lời giải đó :
http://olm.vn/hoi-dap/detail/26954556179.html

Vì \(\left|2x+1\right|\ge0;\left|x+y-\frac{1}{2}\right|\ge0\)
Mà \(\left|2x+1\right|+\left|x+y-\frac{1}{2}\right|\le0\Rightarrow\orbr{\begin{cases}2x+1=0\\x+y-\frac{1}{2}=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-\frac{1}{2}\\y=\frac{1}{4}\end{cases}}\)(1)
Thế (1) vào A
\(\Rightarrow A=4.\left(-\frac{1}{2}\right)^3.\left(\frac{1}{4}\right)^2-\frac{1}{4}.\left(-\frac{1}{2}\right)+2.\frac{1}{4}-5\)
\(\Rightarrow A=-\frac{1}{2}+\frac{1}{8}+\frac{1}{2}-5\)
\(\Leftrightarrow A=\frac{1}{8}-5=\frac{1}{8}-\frac{40}{8}=-\frac{39}{8}\)