Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

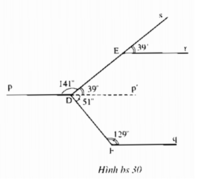
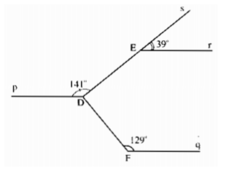
+) Ta có hai đường thẳng DE và DF cắt nhau tại D.
+) Kẻ tia Dp’ là tia đối của tia Dp.
+) Do Er // Dp nên Er // Dp’
Suy ra

+) Ta có tia Dp’ nằm giữa hai tia DF và tia DE nên:
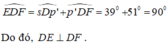

Qua D, kẻ tia Dp' là tia đối của tia Dp.
Vì Er // Dp'
\(\Rightarrow\widehat{sEr}=\widehat{EDp'}\) (2 góc đồng vị)
mà \(\widehat{sEr}=39^0\)
\(\Rightarrow\widehat{EDp'}=39^0\)
Vì Dp' // Fq
\(\Rightarrow\widehat{p'DF}=\widehat{DFq}\)
mà \(\widehat{DFq}=120^0\)
.....

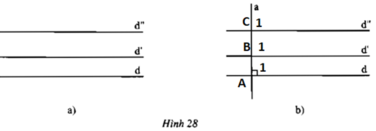
Vì a vuông góc với d ⇒ ∠A1 = 90o
• a có vuông góc với d’
Vì d//d’ ⇒ ∠A1 = ∠B1 ( hai góc đồng vị)
⇒ ∠B1 = 90o
• a có vuông góc với d’’
Vì d//d’’ ⇒ ∠A1 = ∠C1 (hai góc đồng vị)
⇒∠C1 = 90o
• d’ có song song với d’’
Vì ∠B1 = ∠C1 = 90o mà hai góc ở vị trí đồng vị
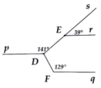
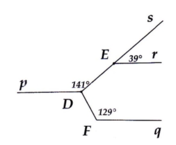
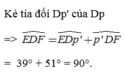


Kẻ tia đối Dp' của Dp => E D F ^ = E D p ' ^ + p ' D F ^ = 39° + 51° = 90°