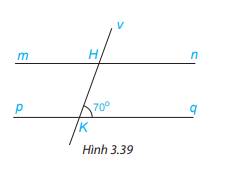
Vì mn//pq nên

+) \(\widehat {mHK} = \widehat {HKq}\) ( 2 góc so le trong), mà \(\widehat {HKq} = 70^\circ  \Rightarrow \widehat {mHK} = 70^\circ \)

+) \(\widehat {vHn} = \widehat {HKq}\) ( 2 góc đồng vị). mà \(\widehat {HKq} = 70^\circ  \Rightarrow \widehat {vHn} = 70^\circ \)

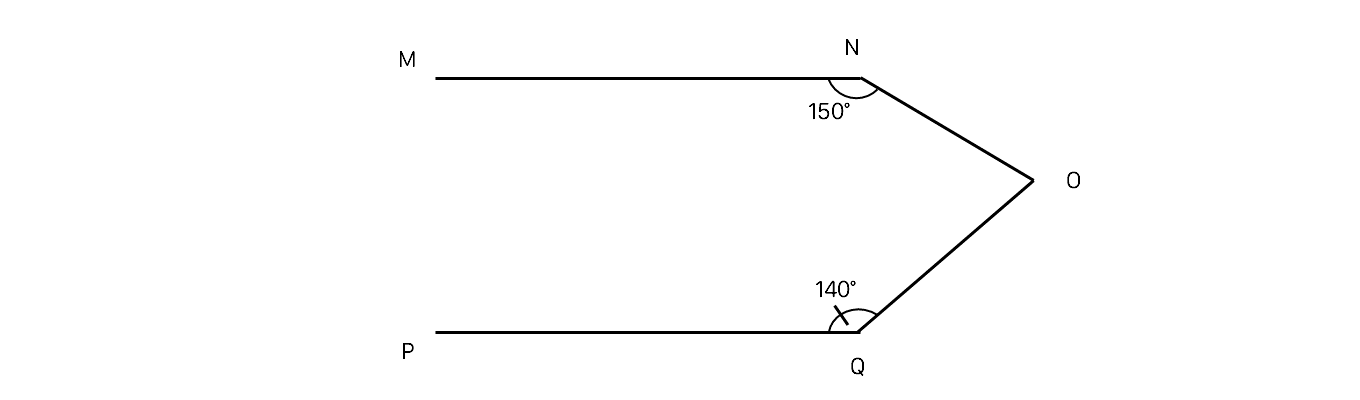
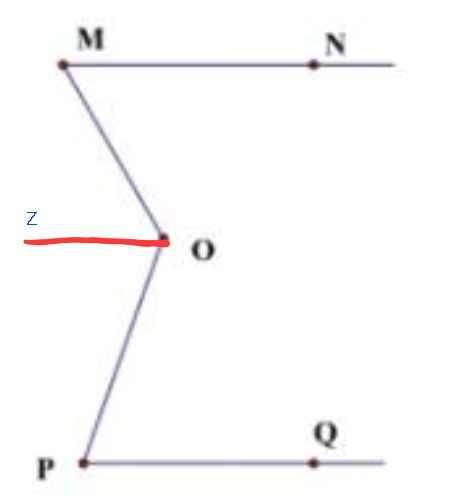  Vẽ tia Oz //MN

⇒ ∠MOz = ∠OMN = 60⁰

⇒ ∠zOP = ∠MOP - ∠MOz

= 130⁰ - 60⁰

= 70⁰

Để MN // PQ thì MN // Oz

⇒ ∠P = ∠OPQ = ∠POz = 70⁰ (so le trong)

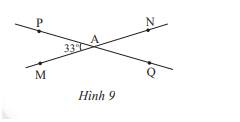
a) Ta có: \(\widehat {PAM} = \widehat {QAN}\) ( 2 góc đối đỉnh) , mà \(\widehat {PAM} = 33^\circ \)nên \(\widehat {QAN} = 33^\circ \)

Vì \(\widehat {PAN} + \widehat {PAM} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {PAN} + 33^\circ  = 180^\circ  \Rightarrow \widehat {PAN} = 180^\circ  - 33^\circ  = 147^\circ \)

Vì \(\widehat {PAN} = \widehat {QAM}\)( 2 góc đối đỉnh) , mà \(\widehat {PAN} = 147^\circ \) nên \(\widehat {QAM} = 147^\circ \)

b)

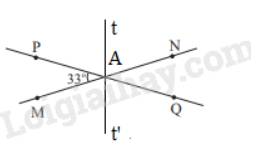
Vì At là tia phân giác của \(\widehat {PAN}\) nên \(\widehat {PAt} = \widehat {tAN} = \frac{1}{2}.\widehat {PAN} = \frac{1}{2}.147^\circ  = 73,5^\circ \)

Vì \(\widehat {tAQ} + \widehat {PAt} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {tAQ} + 73,5^\circ  = 180^\circ  \Rightarrow \widehat {tAQ} = 180^\circ  - 73,5^\circ  = 106,5^\circ \)

Vẽ At’ là tia đối của tia At, ta được \(\widehat {QAt'} = \widehat {PAt}\)( 2 góc đối đỉnh)

Ta có: \(\widehat {QAt'} = \widehat {MAt'} = \frac{1}{2}.\widehat {MAQ}\) nên At’ là tia phân giác của \(\widehat {MAQ}\)

Chú ý:

2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau

a) Ta có: \(\widehat{NAQ}=\widehat{MAP}\)( Hai góc đối đỉnh ) 

Mà \(\widehat{MAP}=30^o\)

\(\Rightarrow\widehat{NAQ}=\widehat{MAP}=30^o\)

b) Ta có: \(\widehat{MAP}+\widehat{MAQ}=180^o\)

\(\Rightarrow\widehat{MAQ}=180^o-\widehat{MAP}\)

\(\Rightarrow\widehat{MAQ}=180^o-30^o\)

\(\Rightarrow\widehat{MAQ}=150^o\)

c) Các cặp góc đối đỉnh là: 

+) \(\widehat{MAP}\)và \(\widehat{NAQ}\)

+) \(\widehat{MAQ}\)và \(\widehat{NAP}\)

d) Các cặp góc bù nhau là: 

+) \(\widehat{MAP}\)và \(\widehat{MAQ}\)

+) \(\widehat{MAP}\)và \(\widehat{NAP}\)

+) \(\widehat{NAQ}\)và \(\widehat{QAM}\)

+) \(\widehat{NAQ}\)và \(\widehat{NAP}\)

b) ∠V2 và ∠U1 là hai góc SLT

⇒ ∠U1 = ∠V2 = 36o.

∠U1 và ∠U2 kề bù

⇒ ∠U1 + ∠U2 = 180o

⇒ ∠U2 = 144o

∠V1 và ∠U2 đồng vị

⇒ ∠V1 = ∠U2 = 144o.

bó tay .com.vn

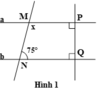
Ta có: a ⊥ P Q ; b ⊥ P Q (gt).

Þ a // b  (vì cùng vuông góc với PQ).

Do đó: x + 75 ° = 180 °  (cặp góc trong cùng phía)

          x = 180 ° − 75 ° = 105 ° .