Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(\overrightarrow{MG}+\overrightarrow{GA}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GB}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GC}\right)^2=GA^2+GB^2+GC^2+12AB^2\)
\(\Leftrightarrow3MG^2+2\overrightarrow{MG}\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)=12AB^2\)
\(\Leftrightarrow MG^2=4AB^2\Leftrightarrow MG=2AB\)
Quỹ tích M là đường tròn tâm G bán kính \(R=2AB\)

a) Gọi O là tâm đường tròn ngoại tiếp. Do tam giác ABC là tam giác đều nên O đồng thời là trọng tâm tam giác đều ABC.
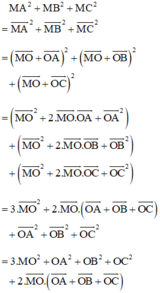
Lại có:
+ O là trọng tâm tam giác nên 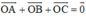
+ Bán kính đường tròn ngoại tiếp tam giác:
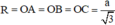
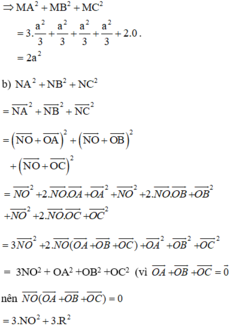
Ta có: NA2 + NB2 + NC2 ngắn nhất
⇔ NO2 ngắn nhất vì R không đổi
⇔ NO ngắn nhất
⇔ N là hình chiếu của O trên d.

Gọi N là trung điểm BC
\(\left|\overrightarrow{MA}+\overrightarrow{MC}+2\overrightarrow{MB}+2\overrightarrow{OC}\right|=\left|\overrightarrow{AB}-\overrightarrow{AD}\right|\)
\(\Leftrightarrow\left|2\overrightarrow{MO}+2\overrightarrow{MB}+2\overrightarrow{OC}\right|=\left|\overrightarrow{AB}-\overrightarrow{AD}\right|\)
\(\Leftrightarrow\left|2\overrightarrow{MC}+2\overrightarrow{MB}\right|=\left|\overrightarrow{AB}-\overrightarrow{AD}\right|\)
\(\Leftrightarrow4\left|\overrightarrow{MN}\right|=\left|\overrightarrow{BD}\right|\)
\(\Rightarrow\left|\overrightarrow{BD}\right|=4\left|\overrightarrow{MN}\right|=4\left|\overrightarrow{DN}+\overrightarrow{MD}\right|\ge4MD-4DN\)
\(\Rightarrow4MD\le BD+4DN\)
\(\Leftrightarrow MD\le\dfrac{BD+4DN}{4}=\dfrac{a\sqrt{2}+2a\sqrt{5}}{4}=\dfrac{2\sqrt{5}+\sqrt{2}}{4}a\)

Gọi M(x, y)
⇒ MA2 = (x – 1)2 + (y – 2)2
MB2 = (x + 3)2 + (y – 1)2
MC2 = (x – 4)2 + (y + 2)2
MA2 + MB2 = MC2
⇔ (x – 1)2 + (y – 2)2 + (x + 3)2 + (y – 1)2 = (x – 4)2 + (y + 2)2
⇔ [(x – 1)2 + (x + 3)2 – (x – 4)2] + [(y – 2)2 + (y – 1)2 – (y + 2)2] = 0
⇔ (x2 – 2x +1 +x2 + 6x + 9 – x2 + 8x -16) + (y2 – 4y + 4 + y2 – 2y + 1 – y2 – 4y – 4) = 0
⇔ (x2 + 12x – 6) + (y2 – 10y + 1) = 0
⇔ (x2 + 12x – 6 +42) + (y2 – 10y + 1+ 24) = 42 +24
⇔ (x2 + 12x + 36) + (y2 – 10y + 25) = 66
⇔ (x + 6)2 + (y – 5)2 = 66.
Vậy tập hợp các điểm M là đường tròn tâm I(–6; 5), bán kính R = √66.


Gọi \(M\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(x-1;y-2\right)\\\overrightarrow{BM}=\left(x+3;y-1\right)\\\overrightarrow{CM}=\left(x-4;y-2\right)\end{matrix}\right.\)
\(MA^2+MB^2=MC^2\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y-2\right)^2+\left(x+3\right)^2+\left(y-1\right)^2=\left(x-4\right)^2+\left(y-2\right)^2\)
\(\Leftrightarrow x^2+y^2+12x-2y-5=0\)
\(\Rightarrow I\left(-6;1\right)\)
Gọi O là tâm hình vuông \(\Rightarrow OA=OB=OC=OD\)
\(\left(\overrightarrow{MO}+\overrightarrow{OA}\right)^2+\left(\overrightarrow{MO}+\overrightarrow{OB}\right)^2+\left(\overrightarrow{MO}+\overrightarrow{OC}\right)^2=3\left(\overrightarrow{MO}+\overrightarrow{OD}\right)^2\)
\(\Leftrightarrow OA^2+OB^2+OC^2+2\overrightarrow{MO}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)=3OD^2+6\overrightarrow{MO}.\overrightarrow{OD}\)
\(\Leftrightarrow\overrightarrow{MO}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}-3\overrightarrow{OD}\right)=0\)
\(\Leftrightarrow\overrightarrow{MO}\left(\overrightarrow{OB}-3\overrightarrow{OD}\right)=0\)
\(\Leftrightarrow\overrightarrow{MO}.\overrightarrow{OB}=0\)
Quỹ tích M là đường thẳng AC