Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này có gì đâu em ! Anh làm nhé !
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE

Bài này có gì đâu em ! Anh làm nhé !
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

Bài 1:
Con tham khảo tại link dươi đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath
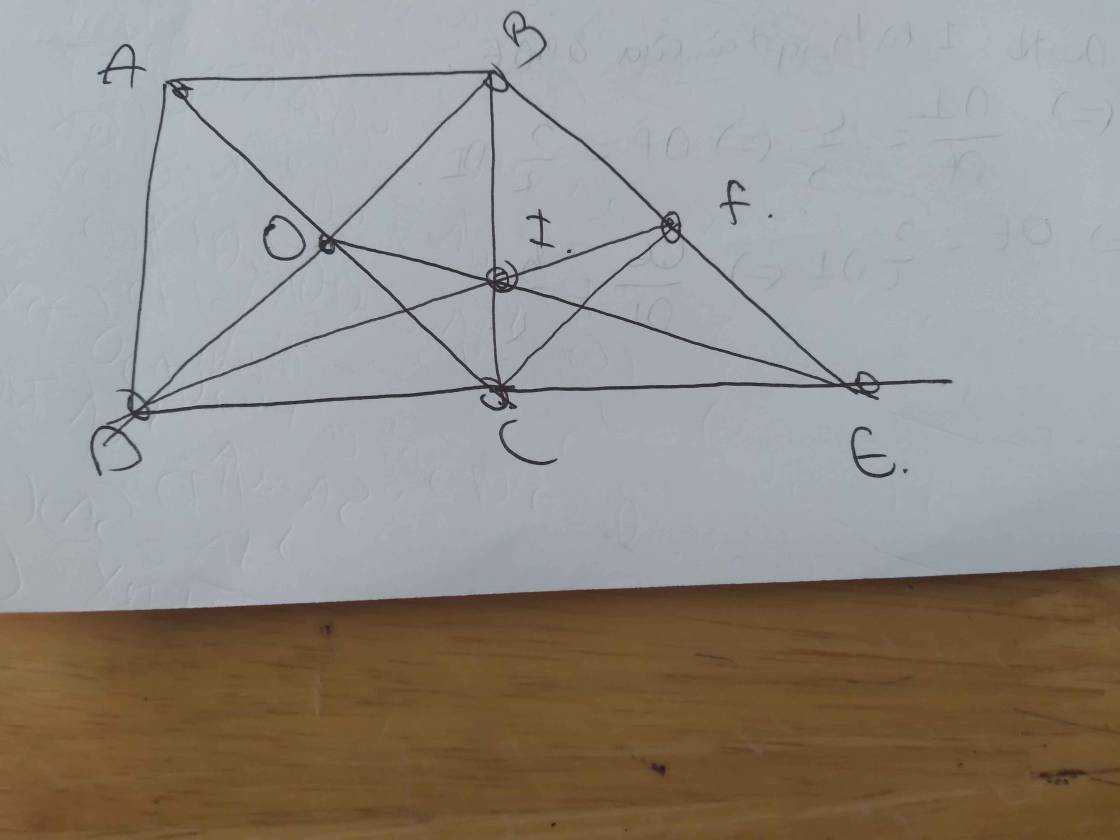




a: AB=DC
DC=CE
Do đó: AB=CE
Xét tứ giác ABEC có
AB//EC
AB=CE
Do đó: ABEC là hình bình hành
b: Xét ΔBDE có
BC là trung tuyến
BC là đường cao
Do đó: ΔBDE cân tại B(1)
Xét ΔBDE có
BC là trung tuyến
\(BC=\dfrac{1}{2}DE\)
Do đó: ΔBDE vuông tại B(2)
Từ (1),(2) suy ra ΔBDE vuông cân tại B
c:
ABCD là hình vuông
=>AC=BD và AC vuông góc với BD tại trung điểm của mỗi đường
=>AC vuông góc BD tại O và O là trung điểm chung của AC và BD
=>OA=OB=OC=OD
Xét ΔBDE có
C,F lần lượt là trung điểm của DE,BE
Do đó: CF là đường trung bình
=>CF//BD và \(CF=\dfrac{BD}{2}\)
=>CF//BO và CF=BO
Xét tứ giác BOCF có
BO//CF
BO=CF
Do đó: BOCF là hình bình hành
mà BO=CO
nên BOCF là hình thoi
Hình thoi BOCF có \(\widehat{OBF}=90^0\)
nên BOCF là hình vuông
d: Xét ΔBDE có
BC,DF là trung tuyến
BC cắt DF tại I
Do đó: I là trọng tâm của ΔBDE
mà O là trung điểm của BD
nên E,I,O thẳng hàng
Xét ΔIDE có
IC là đường cao, là đường trung tuyến
nên ΔIDE cân tại I
=>ID=IE
Xét ΔBDE có
I là trọng tâm
EO là đường trung tuyến
Do đó: \(\dfrac{EI}{EO}=\dfrac{2}{3}\)
=>\(OE=\dfrac{3}{2}EI=\dfrac{3}{2}DI\)
Mình cảm ơn ạ.