Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác ABD và tam giác EBD có
BAD=BED(=90 ĐỘ)
ABD=EBD ( BD là tia pg của ABC)
BD cạnh chug
Do đó t/giác ABD= t/ giác EBD(chgn)
b) Vì t/giác ABC vuông ở A nên
suy ra AB^2+AC^2=BC^2 ( đl PY TA GO)
AB^2+12^2=15^2
AB^2+144=225
AB^2=81
AB^2=9^2
AB=9 cm
Mà AB=BE( t/giác ABD=t/giác EBD)
Do đó BE=9 cm
( sr bạn nhé í c mình chx nghĩ ra![]() ☹)
☹)

a) Xét ΔABN và ΔACM có
AB=AC(ΔABC cân tại A)
\(\widehat{BAN}\) chung
AN=AM(gt)
Do đó: ΔABN=ΔACM(c-g-c)
Suy ra: BN=CM(hai cạnh tương ứng)
b) Xét ΔAHB và ΔAHC có
AB=AC(ΔABC cân tại A)
AH chung
HB=HC(H là trung điểm của BC)
Do đó: ΔAHB=ΔAHC(c-c-c)
Suy ra: \(\widehat{AHB}=\widehat{AHC}\)(hai góc tương ứng)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
hay AH⊥BC(đpcm)
c) Ta có: AH⊥BC(cmt)
mà H là trung điểm của BC(gt)
nên AH là đường trung trực của BC
⇔EH là đường trung trực của BC
⇔EB=EC(Tính chất đường trung trực của một đoạn thẳng)
Xét ΔEBC có EB=EC(cmt)
nên ΔEBC cân tại E(Định nghĩa tam giác cân)

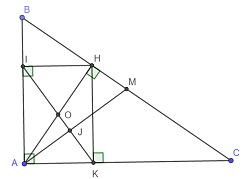
a) Xét tứ giác AIHK có \(\widehat{AIH}+\widehat{IAK}+\widehat{AKH}=270^o\Rightarrow\widehat{IHK}=90^o\)
Vậy nên \(HI\perp HK\)
b) Do IA và HK cùng vuông góc với AC nên IA // HK
Vậy thì \(\widehat{IAH}=\widehat{KHA}\) (So le trong)
Xét tam giác IAH và tam giác KHA có:
\(\widehat{AIH}=\widehat{HKA}=90^o\)
Cạnh AH chung
\(\widehat{IAH}=\widehat{KHA}\)
\(\Rightarrow\Delta AIH=\Delta HKA\) (Cạnh huyền - góc nhọn)
\(\Rightarrow IA=HK.\)
c) Xét tam giác IAH và tam giác HKI có:
\(\widehat{AIH}=\widehat{KHI}=90^o\)
Cạnh IH chung
\(IA=HK\)
\(\Rightarrow\Delta AIH=\Delta KHI\) (Hai cạnh góc vuông)
\(\Rightarrow AH=IK.\)
d) Ta thấy ngay các cặp góc so le trong bằng nhau nên \(\Delta IOA=\Delta KOH\left(g-c-g\right)\Rightarrow OI=OK,OA=OH\)
Xét tam giác vuông IAH có IO là trung tuyến ứng với cạnh huyền nên OH = OA = OI.
Vậy nên OA = OI = OH = OK.
e)
1. Nếu tam giác ABC cân thì AH là đường cao đồng thời trung tuyến. Vậy thì AH = BH = CH.
Xét tam giác cân BHA có HI là đường cao nên đồng thời là đường trung tuyến. Vậy nên I là trung điểm AB.
Hoàn toàn tương tự ta có K là trung điểm AC.
2. Tam giác ABC vuông cân tại A nên \(\widehat{ACB}=45^o\)
IA = AB/2; AK = AC/2 mà AB = AC nên AI = AK.
Vậy thì tam giác IAK cũng vuông cân tại A.
Vậy nên \(\widehat{AKI}=45^o\)
Từ đó ta có \(\widehat{AKI}=\widehat{ACB}=45^o\)
Chúng lại ở vị trí đồng vị nên suy ra IK // BC.
f) Ta có AM = MC nên \(\widehat{MAC}=\widehat{MCA}\)
Lại có \(\widehat{MCA}=\widehat{AHK}\) (Cùng phụ với góc \(\widehat{KHC}\) )
Suy ra \(\widehat{MAC}=\widehat{AHK}\)
Lại có \(\widehat{OKA}=\widehat{OHA}\)
Vậy nên \(\widehat{MAK}+\widehat{OKA}=\widehat{AHK}+\widehat{IHA}=90^o\)
Gọi J là giao điểm của AM và IK thì \(\widehat{AJK}=90^o\) hay \(KI\perp AM\)

a) Xét \(\Delta AHB\)và\(\Delta AHC\)có :
\(\hept{\begin{cases}HB=HC\\AH\\AB=AC\end{cases}}\)( Bạn tự ghi lời giải thích nha)
\(\Rightarrow\Delta AHB=\Delta AHC\left(c.c.c\right)\)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}\)(2 cạnh tương ứng)
Mà \(\widehat{AHB}+\widehat{AHC}=180^o\)( 2 góc kề bù )
\(\Rightarrow\widehat{AHB}=\widehat{AHC}=\frac{180^o}{2}=90^o\)
\(\Rightarrow AH\perp BC\)
b) Xét \(\Delta AHM\left(\widehat{AMH}=90^o\right)\)và \(\Delta AHN\left(\widehat{ANH}=90^o\right)\)có :
\(\hept{\begin{cases}AH\\\widehat{A_1}=\widehat{A_2}\end{cases}}\)( bạn tự nêu lí do )
\(\Rightarrow\Delta AHM=\Delta AHN\)( Cạnh huyền - góc nhọn )

a: Xét ΔNAB có
NM vừa là đường cao, vừa là trung tuyến
nên ΔBAN cân tại N
b: Xét ΔBAC có
M là trung điểm của BA
MN//AC
Do đó: N là trung điểm của BC