Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chứng minh được BF = DH BFDH là hình bình hành (vì BF // DH). Do đó O thuộc FH (vì O phải là giao điểm của hai đường chéo).
b) Dễ thấy (cgv – cgv) nên EF = FG.
Tương tự, FG = GH, GH = HE EF = FG = GH = HE. Suy ra EFGH là hình vuông.
Tương tự phần a) ta chứng minh được O thuộc EG. Từ đó, O là giao điểm hai đường chéo của hình vuông EFGH nên O cách đều E, F, G, H.
c) .
a) Chứng minh được BF = DH BFDH là hình bình hành (vì BF // DH). Do đó O thuộc FH (vì O phải là giao điểm của hai đường chéo).
b) Dễ thấy (cgv – cgv) nên EF = FG.
Tương tự, FG = GH, GH = HE EF = FG = GH = HE. Suy ra EFGH là hình vuông.
Tương tự phần a) ta chứng minh được O thuộc EG. Từ đó, O là giao điểm hai đường chéo của hình vuông EFGH nên O cách đều E, F, G, H.
c) .

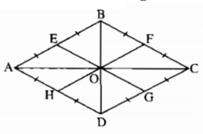
Đặt OB = OD = a. Hãy chứng minh OE = a. Tương tự, OF = OG = OH = a. Từ đó suy ra sáu điểm E, B, F, G, D, H cùng thuộc một đường tròn (O;a).

Đặt OB = OD = a. Hãy chứng minh OE = a
Tương tự, OF = OG = OH = a
Từ đó suy ra sáu điểm E, B, F, G, D, H cùng thuộc một đường tròn ( O;a )
Xét ΔABD có AB=AD và góc BAD=60 độ
nên ΔABD đều
Ta có: ΔDAB cân tại D
mà DE là đường trung tuyến
nên DE vuông góc với BE
=>E nằm trên đường tròn đường kính BD(1)
Ta có:ΔBAD cân tại B
ma BH là đường trung tuyến
nên BH vuông góc với HD
=>H nằm trên đường tròn đường kính BD(2)
Xét ΔCBD có CB=CD và góc BCD=60 độ
nên ΔCBD đều
Ta có: ΔBDC cân tại D
mà DF là đường trung tuyến
nen DF vuông góc với BF
=>F nằm trên đường tròn đường kính BD(3)
Ta có: ΔBDC cân tại B
mà BG là đường trung tuyến
nên BG vuông góc với GD
=>G nằm trên đường tròn đường kính BD(4)
Từ (1), (2), (3) và (4) suy ra E,B,F,G,D,H cùng nằm trên 1 đường tròn

