Cho điểm A nằm ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. lấy điểm B bất kì thuộc đường thằng d. Gọi C là điểm đối xứng với điểm A qua điểm B. Khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào ?

Bài giải:

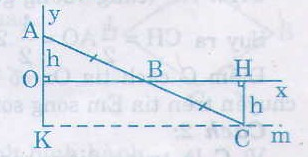
Kẻ AH và CK vuông góc với d.

Ta có AB = CB (gt)

 =  ( đối đỉnh)

nên  ∆AHB =  ∆CKB (cạnh huyền - góc nhọn)

Suy ra CK = AH = 2cm

Điểm C cách đường thẳng d cố định một khoảng cách không đổi 2cm nên C di chuyển trên đường thẳng m song song với d và cách d một khoảng bằng 2cm.

có đúng ko vậy?

Key t chụp ở Câu hỏi của Lưu Đức Mạnh - Toán lớp 8 - Học toán với OnlineMath.Còn hình vẽ là t vẽ nha.câu c đang nghĩ~~~

C,Gọi G là giao điểm của AC và BE

=> \(AG\perp BE\) (C là trực tâm tam giác ABE)

Lại có Góc GAB= Góc GBA = 45 độ

=> tam giác ABG vuông cân 

Mà A,B  cố định

=> G cố định

CMTT câu b  => D;F;G thẳng hàng

=> DF luôn đi qua điểm G cố định khi M di động trên AB
Vậy DF luôn đi qua điểm G cố định khi M di động trên AB

Câu 2: 

a: Xét ΔABC có AD/AB=AE/AC

nên DE//BC

=>BDEC là hình thang

mà góc B=góc C

nên BDEC là hình thang cân

b: Xét ΔDEB có

N là trung điểm của DE

M là trung điểm của DB

Do đó: MN là đường trung bình

=>MN//EB và MN=EB/2(1)

Xét ΔECB có

P là trung điểm của EC

Q là trung điểm của BC

Do đó: PQ là đường trung bình

=>PQ//BE và PQ=BE/2(2)

từ (1) và (2) suy ra MN//PQ và MN=PQ

=>MNPQ là hình bình hành

Xét ΔDEC có

N là trung điểm của DE
P là trung điểm của EC
Do đó: NP là đường trung bình

=>NE=DC/2=NM

=>NMQP là hình thoi

a) Phần thuận:

Vì \(AOBC\)là hình chữ nhật ; M là giao điểm của 2 đường chéo AB và OC

\(\Rightarrow MA=MO\)

Mà \(O;A\)cố định

\(\Rightarrow M\)thuộc đường trung trực của OA.

Vẽ đường trung trực của OA và cắt Ox tại H.

*) Giới hạn: Khi B tiến dần tới O thì M tiến dần tới H.

Nhưng \(B\ne O\)( để tạo thành hình chữ nhật \(AOBC\))

\(\Rightarrow M\ne H\)

Vậy quỹ tích điểm M thuộc tia Ht ( trừ điểm H )

b) Phần đảo :

Lấy M thuộc tia Ht\(\left(M\ne H\right)\)

Tia AM cắt Oy tại B.

Vẽ hình chữ nhật AOBC. Ta phải chứng minh M là giao điểm của 2 đường chéo.

Thật vậy,

Xét tam giác OAB có \(HM//OB\)( Vì cùng vuông góc với Ox )

                \(HA=HO\)( vì Ht là đương trung trực )

\(\Rightarrow M\)là trung điểm của AB.

Mà AOBC là hình chữ nhật

\(\Rightarrow M\)là trung điểm của OC.

\(\Rightarrow M\)là giao điểm của 2 đường chéo.

c) Kết luận: Qũy tích điểm M là tia Ht, trừ điểm H ( Ht thuộc đường trung trực của  OA )