Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: ABCD là hình vuông
=>AB=BC=CD=DA(1)
Ta có: M là trung điểm của AB
=>\(MA=MB=\dfrac{AB}{2}\left(2\right)\)
Ta có: N là trung điểm của BC
=>\(NB=NC=\dfrac{BC}{2}\left(3\right)\)
Từ (1),(2),(3) suy ra MA=MB=NB=NC
Xét ΔMBC vuông tại B và ΔNCD vuông tại C có
MB=NC
BC=CD
Do đó: ΔMBC=ΔNCD
=>\(\widehat{MCB}=\widehat{NDC}\)
mà \(\widehat{NDC}+\widehat{DNC}=90^0\)
nên \(\widehat{MCB}+\widehat{DNC}=90^0\)
=>CM\(\perp\)DN tại I
Ta có: ΔMBC=ΔNCD
=>MC=ND
b: Ta có: AH\(\perp\)DN
CM\(\perp\)DN
Do đó: AH//CM
=>AP//CM
Xét tứ giác AMCP có
AP//CM
AM//CP
Do đó: AMCP là hình bình hành
=>AM=CP
mà \(AM=\dfrac{AB}{2}=\dfrac{CD}{2}\)
nên \(CP=\dfrac{CD}{2}\)
=>P là trung điểm của CD
=>PC=PD
c: Xét ΔDIC có
P là trung điểm của DC
PH//IC
Do đó: H là trung điểm của DI
Xét ΔADI có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔADI cân tại A
=>AD=AI
mà AD=AB
nên AI=AB

Đề sai rồi bạn. E là giao của CM và DN thì E trùng với C rồi bạn
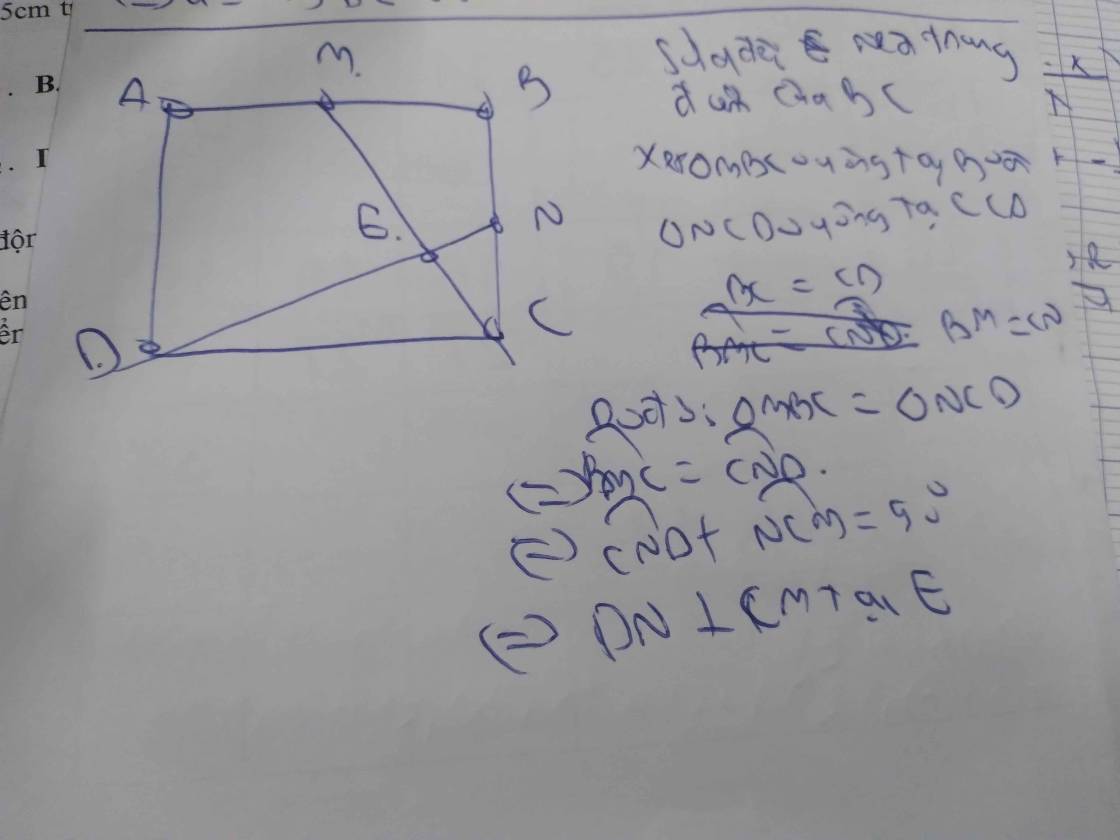
Cho hình vuông ABCD. Gọi M , N lần lượt là trung điểm của AB và BC ĐÂY Ạ

Lấy F trên tia đối của AB sao cho AF=CK
=>AM+CK=AM=MF 3
Xét tam giác DAF và tam giác NCN có
AF=CK(gt)
DAF=DCK(gt DK là pg)
AD=CD(gt)
=> tam giác DAF= tam giác DCK(c-g-c)
=>AFD=CKD( 2 góc t/ứng)
Mà CKD=ADK(slt)=>AFD=ADK 1
Mặt khác ADK= ADM+MDK, MDK=KDC(gt)
=>ADK=ADM+KDC=ADM+ADF 2
Từ 1 và 2=>AFD=ADM+ADF=MDF=>tam giác FMD cân tại M=>FM=MD 4
Từ 3 và 4=>AM+CK=DM
-dpcm-