Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
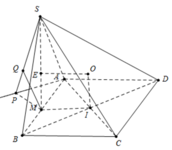
Gọi I và E tương ứng là tâm hình vuông ABCD và tam giác SAB.



Chọn D.
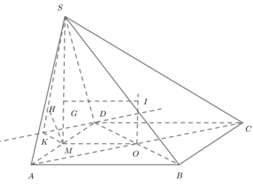
Phương pháp: Xác định cạnh của đáy trước.
Cách giải: Bán kính mặt cầu ngoại tiếp khối chóp là ![]()
Gọi O là tâm của đáy, I là tâm mặt cầu, G là tâm tam giác SAD, M là trung điểm AD.
Dễ thấy I nằm đồn thời trên trục của tam giác SAD và trục của đáy.
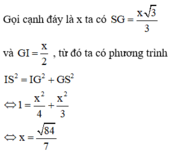
Qua D dựng đường thẳng d song song với AC. Gọi K là hình chiếu cửa M trên d, H là hình chiếu của M trên SD. Suy ra M H ⊥ d , S D .
Ta có:
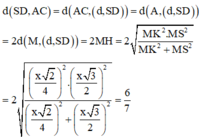

Chọn đáp án D


Thể tích khối chóp N.MCD bằng thể tích khối chóp N.ABCD:

FOR REVIEW |
Tam giác cân có một góc bằng 60 ° thì là tam giác đều. |

Chọn đáp án C
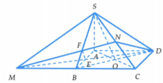
Gọi O là giao điểm của AC và BD
Ta có
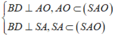
![]()
![]()
⇒ Thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (MND) là tứ giác DEFN.
Suy ra V 1 = V S . A D E F N và V 2 = V B C D E F N
Từ giả thiết ta có ∆ A B D đều cạnh a
![]()
Thể tích khối chóp N.MCD là
V N . M C D = 1 3 d N ; M C D . S ∆ M C D = a 3 4
Ta có F là trọng tâm của ∆ S M C nên M F M N = 2 3 ; E là trung điểm của MD nên M E M D = 1 2
Áp dụng công thức tính thể tích ta có:
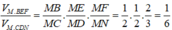
![]()
Thể tích khối chóp S.ABCD là
V S . A B C D = 1 3 . S A . S A B C D = a 3 4
Suy ra V 1 = V S . A D E F N = V S . A B C D - V 2 = a 3 24
Vậy V 1 V 2 = 1 5


Gọi E là trung điểm của AD ta chỉ ra mặt cầu ngoại tiếp hình chóp S.ABC cũng là mặt cầu ngoại tiếp hình
chóp S.EABC .
Từ đó ta đưa về bài toán tìm bán kính của mặt cầu ngoại tiếp hình chóp có cạnh bên vuông góc với đáy.
Sử dụng công thức tính nhanh
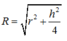
với R là bán kính mặt cầu ngoại tiếp hình chóp, r là bán kính
đường tròn ngoại tiếp đáy hình chóp, h là chiều cao hình chóp
Sử dụng công thức tính diện tích mặt cầu

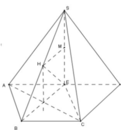
Mà SE vuông góc với AD (do tam giác SAD đều có SE là trung tuyến)
Suy ra SE vuông góc với ( ABCD)=>SE vuông góc với (EABC)
Nhận thấy EABC là hình vuông nên đường tròn ngoại tiếp EABC cũng
là đường tròn ngoại tiếp tam giác ABC
Hay mặt cầu ngoại tiếp hình chóp S.ABC cũng là mặt cầu ngoại tiếp hình chóp S.EABC.
Mà hình chóp S.EABC có cạnh bên SE vuông góc với (EABC) và đáy EABC là hình vuông cạnh a. Gọi I là tâm hình vuông EABC
Suy ra bán kính mặt cầu ngoại tiếp chóp S.EABC là



Ta có S C D ∩ A B C D = C D
C D ⊥ S A C D ⊥ A C ⇒ C D ⊥ S A C ⇒ S C ⊥ C D
Vì S C ⊥ C D , S C ⊂ S C D A C ⊥ C D , A C ⊂ A B C D
Nên S C D , A B C D ^ = S C A ^ = 45 o
Dễ thấy ∆ S A C vuông cân tại A
Suy ra SA = AC = a 2
Lại có
S M C D = 1 2 M C . M D = 1 2 a . a = a 2 2
Do đó
V = V S . M C D = 1 3 S M C D S A = 1 3 . a 2 2 . a 2 = a 3 2 6
Ta có
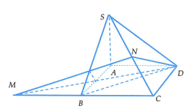
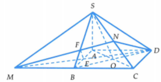
B D ∥ M N M N ⊂ S M N ⇒ B D ∥ S M N
Khi đó d( SM,BD ) = d( SM, (SMN) ) = d( D, (SMN) ) = d( A, ( SMN) )
Kẻ A P ⊥ M N , P ∈ M N A H ⊥ S P , H ∈ S P
Suy ra A H ⊥ S M N ⇒ d A S M N = A H
∆ S A P vuông tại A có
1 A H 2 = 1 S A 2 + 1 A P 2 = 1 S A 2 + 1 A N 2 + 1 A M 2 = 1 2 a 2 + 1 a 2 4 + 1 a 2 = 11 2 a 2
Do đó d = d( SM, BD ) = AH = a 22 11
Đáp án A








Đáp án D
Gọi O là tâm hình vuông ABCD
G là trọng tâm tam giác đều SBC
Đường thẳng qua O vuông góc với (ABC cắt đường thẳng qua G vuông góc với (SBC) tại I
Khi đó R S . A B C D = S I = G I 2 + O H 2 = S 4 π
Đặt A D = A B = a ⇒ S G = a 3 3 ; O H = a 2
Suy ra a 2 3 + a 2 4 = 21 ⇒ a = 6
Dựng A x / / B D ; H E ⊥ A x , H F ⊥ S A E ⇒ d B D ; S A = d B ; S A x = 2 d H = 2 E F
Lại có A E = A H sin 45 ° = 3 2 2 ; S H = 3 3 ⇒ H F = S H . H E S H 2 + H E 2 = 2 21 7
Do đó d S A ; B D = 6 21 7